Paralelno računanje števila Pi (π)

Aproksimacija števila π se lahko dobi z naslednjim približkom

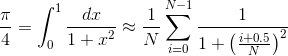
kjer se odgovor dobi s približkom, ki postaja boljši z naraščajočim N. Iteracije so med seboj neodvisne od i in s tem jih je tako možno paralelizirati. Za naslednje primere uporabite N=2310, ki je deljivo z 2,3,4,5,6,7,8,9,10,11 in 12

1. Popravite hello.py tako, da bo vsak proces neodvisno izračunal vrednost π in ga izpisal na zaslon

   # -*- coding: utf-8 -*- pi0.py
   
   from mpi4py import MPI
   
   comm = MPI.COMM_WORLD
   
   size = comm.Get_size()
   
   rank = comm.Get_rank()
   
   N = 2310
   
   vsota=0.0
   
   for i in range(N):
   
       vsota += 1/(1+((i+0.5)/N)**2)
   
   print "Pi = ", 4*vsota/N
   

2. Sedaj uporabite različne procese, da bodo po delih izračunali vsoto. Če imamo samo dva procesa, potem bo rank  0 izračunal i v mejah od i=0,1,N/2-1 ter rank 1 v mejah i=N/2..N-1. Program poženemo z ukazom

   half mpirun -np 2 python pi1.py
   

   Upoštevajte, da je

   range([start,] stop[, step]) -> list of integers
   

   Na roke seštejte in preverite, če so delne vsote pravilne.

   # -*- coding: utf-8 -*- pi1.py
   
   from mpi4py import MPI
   
   comm = MPI.COMM_WORLD
   
   size = comm.Get_size()
   
   rank = comm.Get_rank()
   
   N = 2310
   
   vsota = 0.0
   
   start = rank*N/size
   
   stop = (rank+1)*N/size
   
   for i in range(start, stop):
   
       vsota += 1/(1+((i+0.5)/N)**2)
   
   print "%f rank %d [%d,%d]" % (4*vsota/N, rank, start, stop)
   

   Za večje število procesov uporabimo awk

   node mpirun -np 11 python pi1.py|awk '{sum+=$1}END{print "Pi=",sum}'
   

3. Sedaj želimo v glavnem procesu (rank 0) sešteti vse delne vsote tako da
   • Vsi procesi razen glavnega pošljejo svojo delno vsoto glavnemu procesu
   • Glavni proces sprejme v vrednosti vseh ostalih procesov in jih sešteje v zanki
   Uporabiti morate MPI ukaza za pošiljanje in sprejemanje

   # -*- coding: utf-8 -*- pi2.py
   
   from mpi4py import MPI
   
   comm = MPI.COMM_WORLD
   
   size = comm.Get_size()
   
   rank = comm.Get_rank()
   
   N = 2310
   
   vsota = 0.0
   
   start = rank*N/size
   
   stop = (rank+1)*N/size
   
   for i in range(start, stop):
   
       vsota += 1/(1+((i+0.5)/N)**2)
   
   
   
   if rank == 0:
   
       for i in range(1, size):
   
           vsota += comm.recv(source=i, tag=1)
   
       print "Pi =", 4*vsota/N
   
   else:
   
       comm.send(vsota, dest=0, tag=1)

4. Zagotovite, da program deluje pravilno tudi če N ni natančno mnogokratnik procesov P.
5. Namesto po blokih raje uporabite preskoke (stride oziroma step) v ukazu range()
6. Uporabite redukcijo za delne vsote

   #..
   
   pi = comm.reduce(vsota, op=MPI.SUM, root=0)
   
   if rank == 0:
   
       print "Pi =", 4*pi/N

7. Potem ko ste izračunali vsoto Pi jo pošljite še vsem procesom z

   pi = comm.bcast(vsota, root=0)
   

8. Uporabite funkcijo MPI.Wtime() za merjenje stenčasa. Funkcijo je potrebno klicati na začetku in potem še na koncu izračunati razliko. S tem lahko tudi preverimo ali je koda pravilno balansirana po procesorjih. Na primer

   t0 = MPI.Wtime()
   
   #... računamo
   
   print "preteklo =", MPI.Wtime() - t0

9. Preverite ali v primeru da v zanki glavnega procesa sprejemate rezultate v poljubnem vrstnem redu tako, da rečete

   vsota += comm.recv(source=MPI.ANY_SOURCE, tag=1)
   

   deluje hitreje kot če zahtevate natančen vrstni red. Koliko procentov hitreje je wildcard sprejem? Poskusite ponoviti izračun večkrat, da dobite boljši povprečni rezultat. Kaj pa če naredimo dva dela kode, ki se hkrati izvajata in vsak računa svoj Pi. Ali lahko to potem ločimo v wildcard z izbiro tag-a?
10. Primerjajte aproksimacijo z

    import math
    
    #..
    
    error = pi - math.pi