Main menu
Nahajate se tukaj
Razširitev nekolizijskih razelektritvenih modelov za aplikacijo v fuzijsko relevantnih in splošnih plazmah
Razširitev nekolizijskih razelektritvenih modelov za aplikacijo v fuzijsko relevantnih in splošnih plazmah
Leon Kos, Nikola Jelić, Jožef Duhovnik, Siegbert Kuhn*, D.D.Tskhakaya*
Laboratorij za računalniško podprto konstruiranje - LECAD
Fakulteta za strojništvo
Univerza v Ljubljani
*Univerza v Innsbrucku, Institut za teoretično fiziko.
Projekt predstavlja matematično-numerično razširitev nekolizijskih razelektritvenih modelov v široka temperaturna območja in za primere končne debeline plazemskega plašča, ki omogočajo izpopolnjene aplikacije v fuzijsko relevantnih in splošnih plazmah. Prispevke dela lahko strnemo na: (i) Obstoječi model je razširjen s tako imenovanim končnim ε=λD/L, kar pomeni, da kvazi-nevtralnost ni striktno zagotovljena, temveč se uporablja kompletna Poissonova enačba namesto pogoja kvazinevtralnosti. (ii) Določanje jedra je bilo izvedeno z neposredno z uporabo splošnih programskih knjižnic. Profil potenciala je določen z zgoščeno mrežo na samo ob steni, temveč tudi v središču simetrije tako, da se bo uporabila adaptivna metoda. (iii) Osnovne hidrodinamske količine, kot so ionska gostota, ionski fluks, ionska energija in temperatura, so bili izpeljani neposredno iz porazdelitve hitrosti na mreži z integracijo, ki je samoadaptivna v bližini singularnosti jedra integrala, kot tudi v bližini singularnosti električnega polja oz. inverzne vrednosti. (iv) Izvedena sta dva modela, in sicer v širokem spektru ionskih temperatur z upoštevanjem končne vrednosti ε in v limitnem primeru ε = 0.
Uvod
Postavitev roba kvazi-nevtralne plazme, tj. meje (ali roba) plašča, je star, vendar še vedno nezadostno rešen problem, ki je pomemben za fuzijo kot tudi za laboratorijske plazme in plazme v vesolju. Meja plašča je površina, do katere lahko predpostavimo kvazi-nevtralnost. Predplašč lahko modeliramo z uporabo fluidnih aproksimacij (namesto vpeljave računsko zahtevnih kinetičnih modelov) z relevantnimi mejnimi pogoji na začetku plašča. Vendar je mejno površino še vedno nemogoče določiti z zadostno natančnostjo. Meja plašča se lahko dovolj natančno določi le v asimptoti dvodelne limite. Pri taki aproksimaciji se lahko meja plašča veže na stran plazme (neskončno tanek plašč) kot mesto singularnosti električnega polja (znameniti Tonksov in Langmuirov model iz leta 1929) ali na stran plašča (neskončno velik plašč) kot mesto izginjanja električnega polja (znameniti Bohmov model iz leta 1949). Oba modela sta bila prvotno izpeljana za primer ``mrzlega'' vira ionov (ioni, ki so narejeni v plazmi z zanemarljivimi hitrostmi v primerjavi s hitrostmi elektronov) in sta bila kasneje razširjena v splošno sprejeti izraz, ki pravi, da je rob plašča mesto, na katerem povprečna ionska hitrost v smeri x (pravokotni na steno) večja ali enaka lokalni ionski zvočni hitrosti..
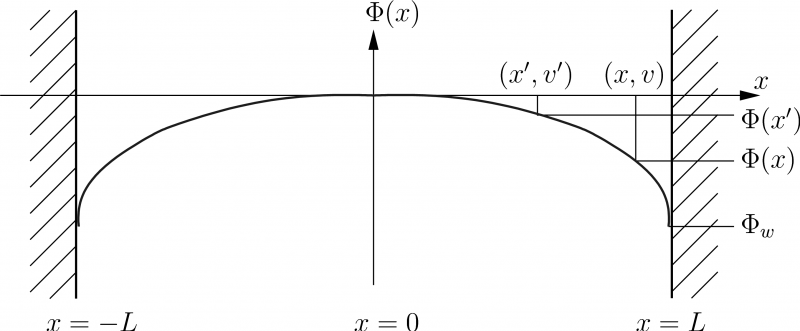
Slika 1: Koordinatni sistem problema
Ob koncu prejšnjega stoletja so bili poskusi reševanja dvodelnega problema za primer ``porazdelitve hitrosti toplega vira ionov'', tj. za primer, ko je temperatura vira ionov primerljiva s temperaturo pripadajočih elektronov. V takem primeru Fredholmove enačbe modela ni možno analitično rešiti, razen v primeru, da vnaprej predpišemo posebno obliko porazdelitve ionskega vira, za katerega je možen analitičen rezultat. Prvotna izpeljava fizikalnega problema v Bissllovem in Johnsonovem
modelu vodi v splošna integralno enačbo problema:
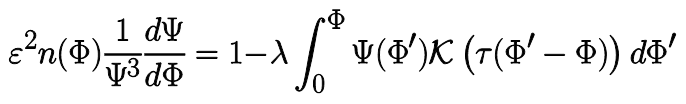
v katerem je neznana funkcija v in izven integrala. Ta integro-diferencialna enačba se lahko šteje kot posplošitev enačb Fredholmovega tipa, ki ni ne prve ne druge vrste, marveč je očitno nelinearna in v literaturi ni klasificirana. Vendar celo v dvodelni aproksimaciji končne porazdelitve ionov ni bilo moč izračunati za poljubno temperaturo vira ionov, saj je bilo singularno jedro integralne enačbe neprimerno za numerične izračune.
Rezultati
Avtor je bil dolgo časa vključen v izkoriščanje paralelnih računalniških kapacitet povezanih s fuzijskimi raziskavami z namenom optimizacije Evropskih računalniških virov. Njegovo sodelovanje v projektu EUFORIA je zahtevalo poglobljeno vključevanje pri preizkušanju nekaterih zahtevnih problemov v plazmi. Ker je bila Bissllova in Johnsonova enačba za ta namen velik izziv, je začel razvijati svoje programske pakete za rešitev problema. Tako pričakujemo, da bo pričujoča disertacija pomembno prispevala k fuzijski skupnosti z nadgradnjo obstoječih rezultatov.
Rešitev zgoraj predstavljenega problema ima velik pomen za fuzijo in splošno plazmo. Pri uporabi fluidnih kod, kot sta npr. SOLPS in EDGE-2D, namenjena za simulacije v področju Scrape-Off Layer (SOL) TOKAMAK naprav, je namreč potrebno določiti meje računskega območja. Robnih pogojev se na osnovi teorije fluidov ne da določiti natančno, saj je potrebno uporabiti še kinetično teorijo. Rezultati iz kinetične teorije, ki predpostavlja toplo ionsko populacijo, pa zahtevajo obsežne računske vire.
Rešitev enačbe za primer ε = 0 prikazuje slika 2. Primerjave profilov potencialov z B&J in S&E modelom so pokazale dobro ujemanje v območjih, kjer so le-ti veljavni. Profil potenciala predstavlja ``prstni odtis'' za vse nadaljnje izračune pomembnih količin v fiziki plazme.
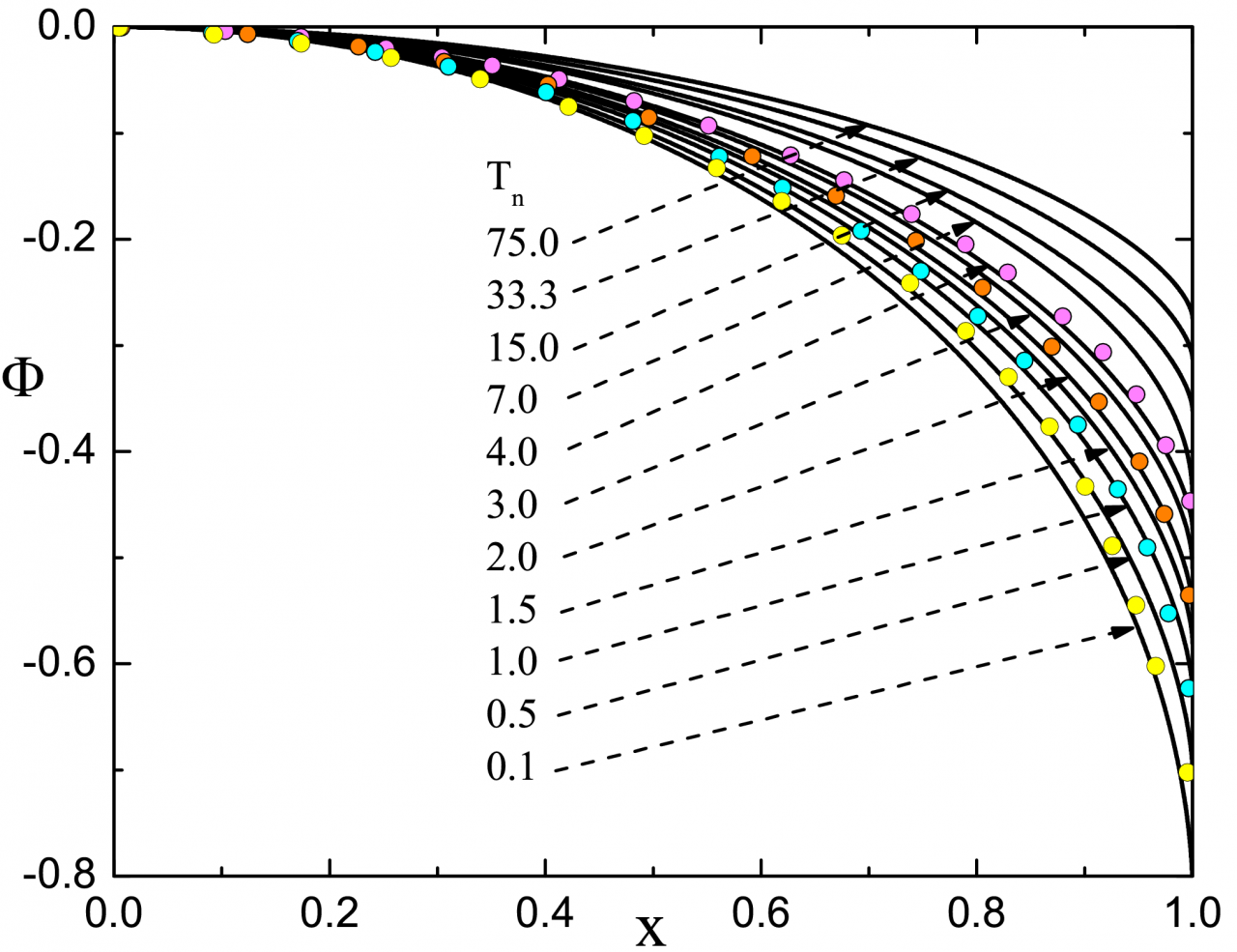
Slika 2: Profili potencialov v razširjenem območju temperatur ionskih virov pri ε = 0, kot smo jih izračunali z našo analitično-numerično metodo (polne črte) v primerjavi z ozkim območjem Bissllovega in Johnsonovega modela (pikčasto).
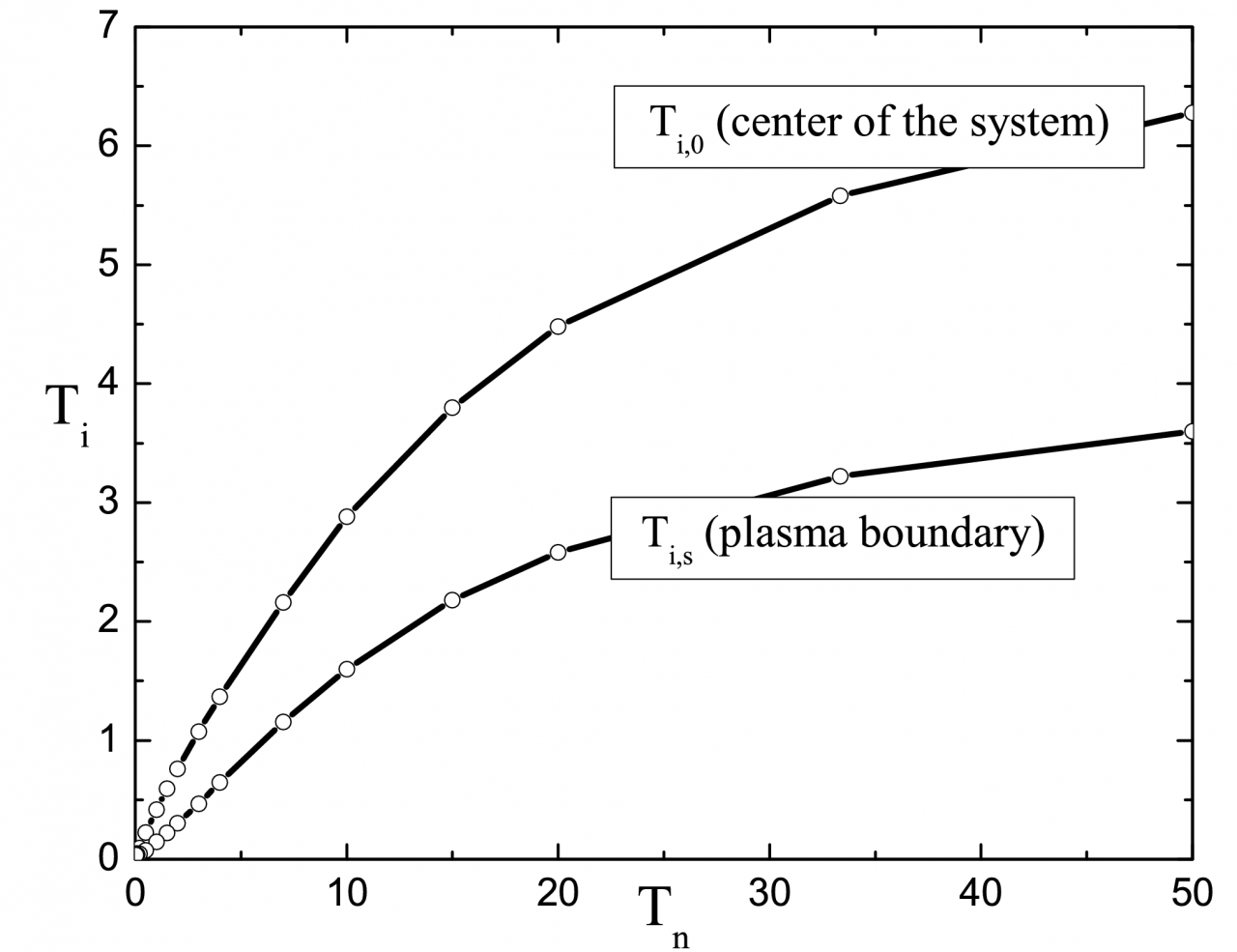
Slika 3: Odvisnost temperature ionov od temperature ionskega vira v plazmi in na plašču kaže na bistveno ohladitev plazme v primerjavi z virom. To pomeni, da je za fuzijsko relevantne plazme potrebno zagotoviti za nekajkrat toplejše vire, da dosežemo ustrezno temperaturo potrebno za fuzijsko reakcijo s pozitivnim dobitkom.
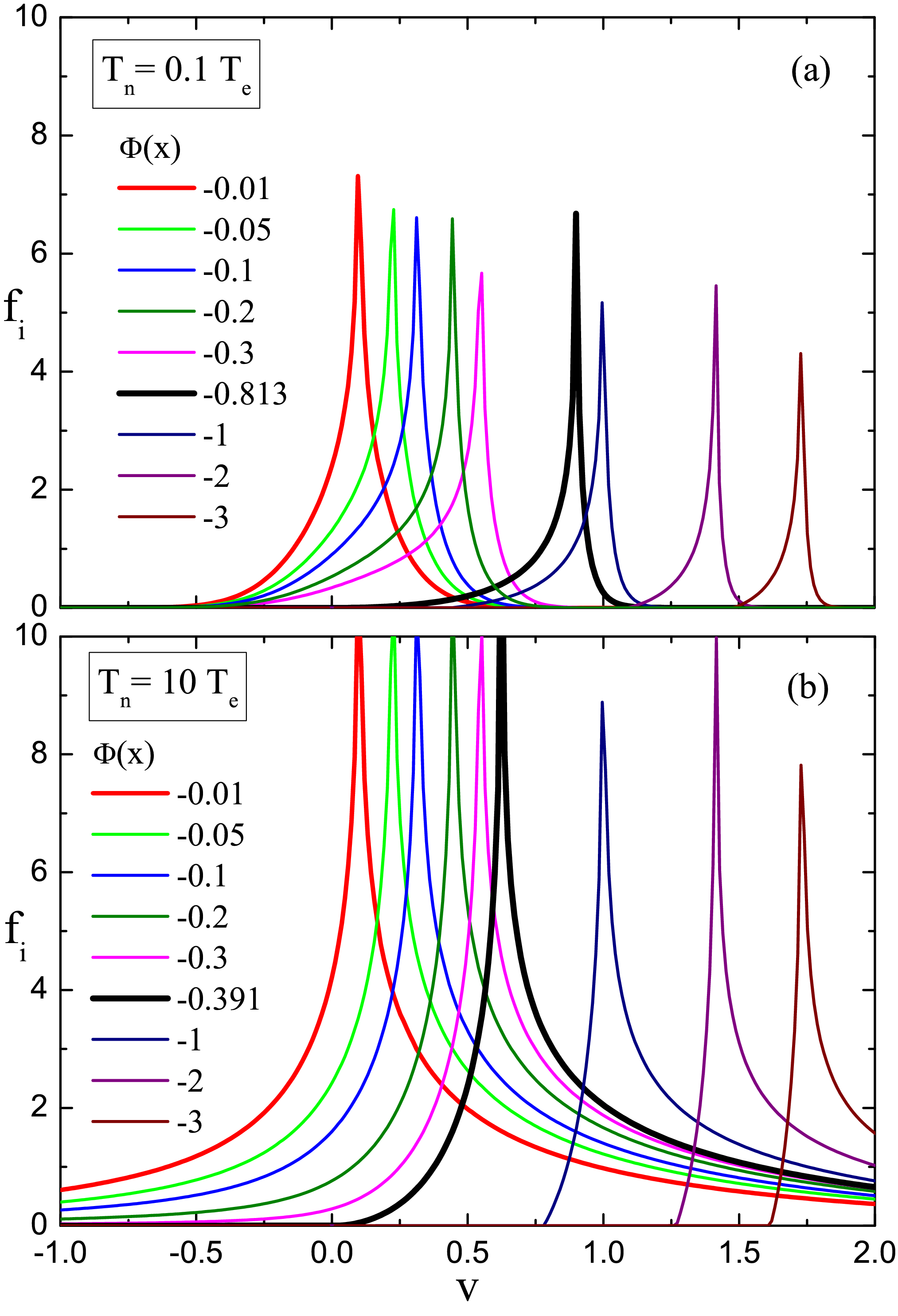
Slika 4: Porazdelitve hitrosti ionov (VDF) za (a) Tn=0.1 kar ustreza "laboratorijskim" plazmam in (b) Tn=10 ustreza fuzijsko relevantnim plazmam. Iz porazdelitev je razvidno, da na plazemskem plašču (Phi=0.391) naenkrat zmanjka ionov z negativnimi hitrostmi, kar bi lahko definirali kot nov kriterij za določitve prehoda med plazmo in plaščem. Pomemno je tudi razbrati s primerjavo porazdelitve hitrosti dveh različnih temperatur ionskih virov, da se z višanjem temperature Tn > 1 spremeni tudi oblika porazedlitve hitrosti - oblika porazdelitve se obrne.
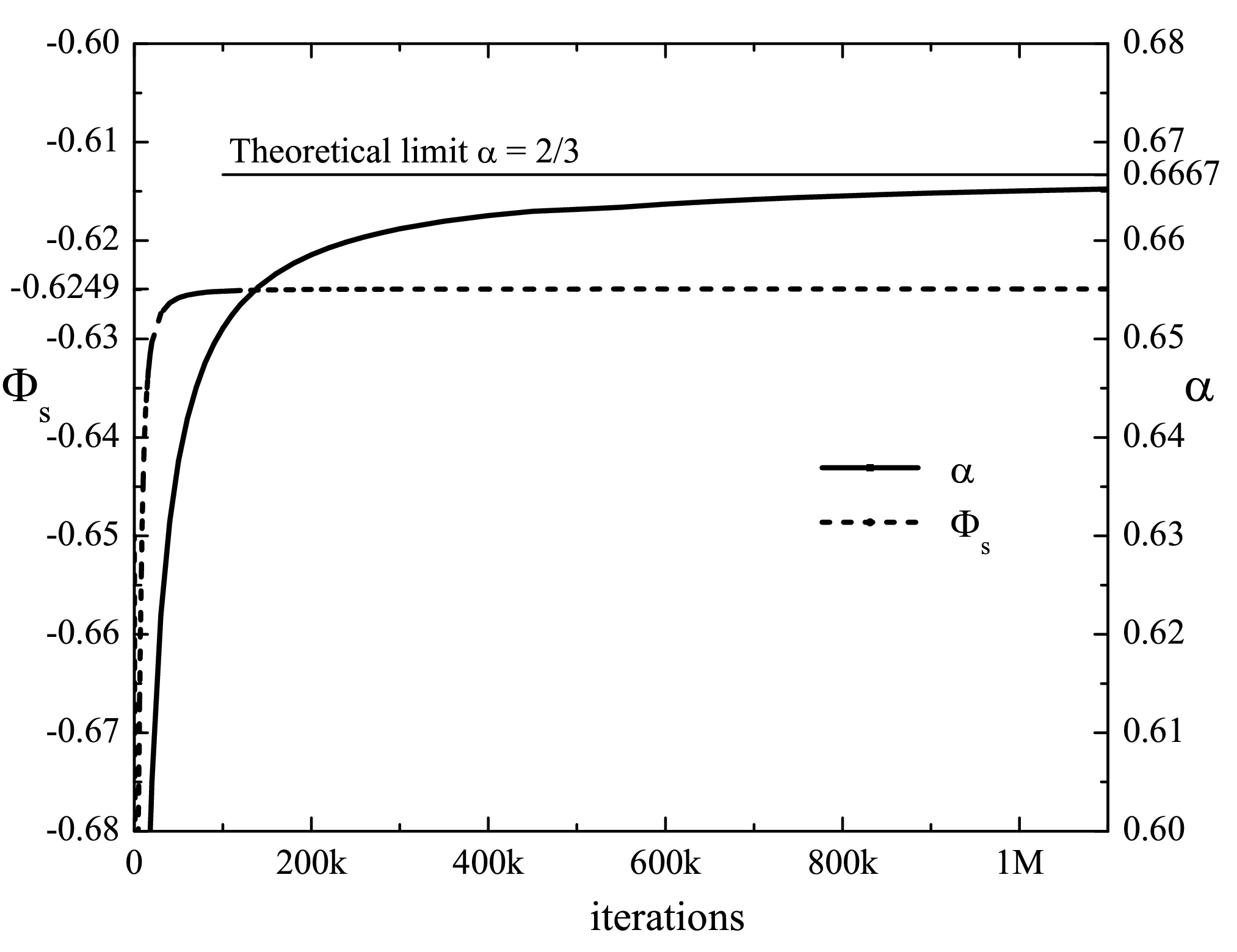
Slika 5: Konvergenca eksponenta alpha, ki karakterizira tip singularnosti plazemskega plašča. Medtem ko je potencial na plašču Phis skonvergiral v 100000 iteracijah, je za dokončno konvergenco potrebno več kot milion iteracij za kar je bilo porabljeno 3 mesece računanja na 16 procesorskem računalniku! Prikazana je le konvergenca ene točke pri temperaturi Tn=1. Za določitev grafa v celotnem območju Tn = [0.01, 100] je bilo porabljenih več kot 700000 procesorskih ur na superračunalniku LEO1 univerze v Innsbrucku.
Hitrostni testi
Razvita programska koda je za namene primerjave različnih superračunalnikov služila tudi za izbor arhitekture HPCFS. Ker je koda predvsem računsko intenzivna se je izkazalo, da vključeno nitkanje z navideznimi jedri (hyperthreading) na procesorjih Intel bistveno pomaga k hitrosti izračunavanja. Pospešek zaradi hyerthreadinga je lahko tudi do 50%. Teste smo izvajali tudi na naslednjih evropskih sestavih:
- EFDA-ITM Gateway - AMD 2352 (Barcelona) - http://www.efda-itm.eu/
- Mellanox inc. Cluster - Vesta - AMD AMD 6136 (Magny cours) - http://www.hpcadvisorycouncil.com/cluster_center.php
- Juelich supercomputing centre - Cluster HPC-FF- Intel X5570 (Nehalem-EP) - http://www.fz-juelich.de/jsc/juropa/
- Univerza v Innsbrucku - LEO1 - AMD 6172 (Opteron)- http://www.uibk.ac.at/zid/systeme/hpc-systeme/leo1/
| CPU | AMD 6172 @2.1GHz Open64 -O3 | AMD 6172 @2.1GHz ICC 11.1 -O2 |
AMD 2352 @2.1GHz ICC 11.0 -O3 |
AMD 2352 @2.1GHz GCC 4.1.2 -O3 | AMD 2352 @2.1GHz Open64 4.2.3 -O3 | Intel X5570 @2.93GHz ICC 11.1 -O2 | Intel X5570 @2.93GHz GCC 4.3.2 -O3 |
AMD 6176SE @2.3GHz /skalirano *1.095 |
AMD 6136 @2.4HGHz /skalirano *1.142 |
| 1 | 67.1 / 0.89 | 53.7 / 1.11 | 64.5 / 0.93 | 69.5 / 0.86 | 68.1 / 0.88 | 25.7 / 2.33 | 28.9 / 2.07 | / 1.21 | 47.6 / 1.26 |
| 2 | 33.92 / 1.76 | 27.4 / 2.19 | 38.4 / 1.56 | 41.7 / 1.44 | 40.1 / 1.50 | 13.13 / 4.57 | 14.7 / 4.08 | ||
| 3 | 22.83 / 2.62 | 18.5 / 3.24 | 26.4 / 2.27 | 28.0 / 2.14 | 27.3 / 2.20 | 8.71 / 6.89 | 9.76 / 6.15 | ||
| 4 | 17.23 / 3.48 | 13.9 / 4.31 | 18.4 / 3.26 | 19.9 / 3.01 | 19.0 / 3.16 | 6.51 / 9.22 | 7.33 / 8.19 | ||
| 6 | 11.46 / 5.23 | 9.25 / 6.49 | 11.9 / 5.04 | 12.5 / 4.80 | 12.4 / 4.83 | 4.36 / 13.8 | 4.88 / 12.3 | ||
| 8 | 8.70 / 6.90 | 6.98 / 8.60 | 8.21 / 7.30 | 8.86 / 6.77 | 8.69 / 6.90 | 3.25 / 18.5 | 3.72 / 16.1 | 6.37/ 9.41 | 6.12 / 9.8 |
| 12 | 5.75 / 10.43 | 4.62 / 12.98 | ~2.16 / ~27.8 (1) |
||||||
| 16 | 4.37 / 13.72 | 3.48 / 17.24 | 3.04 / 19.7 | ||||||
| 24 | 2.85 / 21.05 | 2.31 / 25.97 | ~1.37 / ~43.6 (2) | 2.1 / 28.44 | |||||
| 32 | ~1.5 / ~39.4 | ||||||||
| 48 | ~1.15/~51.94 | 1.05 / 56.9 |
(1) Projekcija za X5670 - skalirano z 12/8
(2) Projekcija s hyperthreadingom *1.57
Primerjalna tabela kaže na naslednje pomembne ugotovitve:
- Med -O2 in -O3 za Intel 11.1 prevajalnik ni nikakršne razlike.
- Na Xeon procesorjih je ICC okoli 15% hitrejši od GCC
- Na AMD procesorjih je ICC okoli 8% hitrejši od GCC
- Na AMD procesorjih je Open64 okoli 2% hitrejši od GCC
- AMD Magny-Cour je pri isti frekvenci 20% hitrejši od Barcelone
- 12 Xeon jeder s HT je približno isto zmogljivo kot 32 Opteron jeder
Zaključek
V razširjenem modelu smo vpeljali natančno jedro in hkrati povečali ločljivost in gostoto mreže in z dodatnimi stabilizacijskimi ukrepi izboljšali konvergenco. Za potrditev numerične stabilnosti in natančnosti so bili rezultati preverjeni v Mathematici in v naši programski kodi, ki so izkazali odlično ujemanje v vseh numeričnih
rezultatih. S fizikalnega stališča smo ugotovili, da je končna ionska temperatura veliko manjša od temperature ionskega vira. Ta ugotovitev je zelo pomembna v fuzijskih napravah, kjer ioni prehajajo iz jedra (CORE) v področje SOL, kjer se ob približevanju divertorjem na hitro ohladijo. Kot najpomembnejše smo našli mejo plazme xs kot funkcijo temperature ionskih virov. Pokazali smo, da v plazmah s končno temperaturo ionskih virov maksimum politropičnega koeficienta ne sovpada z robom plašča plazme, kot je to praviloma pri plazmah z zanemarljivo majhnimi temeraturami ionskih virov, vendar jih lahko še vedno obravnavamo kot dober približek za mejo med plazmo in plaščem. To dejstvo je lahko pomembno pri povezovanju fluidnih in kinetičnih parametrov plazme v fluidnih kodah, kot jenpr. SOLPS-B2.
Nagrade
Za znanstveno odličnost dela je bila Leonu Kosu podeljena nagrada Trimo Research Award 2010.

Bibliografija
- Leon Kos, Nikola Jelić, Siegbert Kuhn, Jože Duhovnik, Complete plasma and sheath solution for Tonks-Langmuir models with warm ion sources, 37th EPS Conference on Plasma Physics, Dublin, Ireland, 2010, http://ocs.ciemat.es/EPS2010PAP/pdf/P5.408.pdf
- KOS, Leon, JELIĆ, Nikola, KUHN, Siegbert, DUHOVNIK, Jože. Extension of the Bissell-Johnson plasma-sheath model for application to fusion-relevant and general plasmas. Phys. plasmas, 2009, vol. 16, iss. 9, str. 093503-1-093503-14, ilustr. http://www.lecad.fs.uni-lj.si/~leon/research/ppgplasma/PHPAEN169093503_1.pdf, doi: 10.1063/1.3223556. [COBISS.SI-ID 11092763], IF=2.43
- JELIĆ, Nikola, KOS, Leon, TSKHAKAYA, D.D., DUHOVNIK, Jože. The ionization length in plasmas with finite temperature ion sources. Phys. plasmas, 2009, iss. 12, vol. 16, str. 123503-1-123503-9, ilustr. http://lecad.fs.uni-lj.si/~leon/research/ppgplasma/PHPAEN1612123503_1.pdf, doi: 10.1063/1.3271412. [COBISS.SI-ID 11223323], IF=2.43
- Leon Kos, Extension of Collisionless Discharge Models for Application to Fusion-Relevant and General Plasmas, PhD, University of Ljubljana, 2009, http://lecad.si/~leon/research/ppgplasma/ppgplasma.pdf
- Leon Kos, Jože Duhovnik, and Nikola Jelić. Extension of collisionless discharge models for application to fusion-relevant and general plasmas. In Proceedings of the International Conference Nuclear Energy for New Europe 2009, pages 820.1-820.10. Nuclear society of Slovenia, 2009. http://www.djs.si/bled2009/.
- Leon Kos, Nikola Jelić, and Jože Duhovnik. Modelling the plasma-sheathboundary for plasmas with warm-ion sources. In Proceedings of the International Conference Nuclear Energy for New Europe, pages 807(1){807(8), Portorož, Slovenia, 2008. Nuclear society of Slovenia. http://www.nss.si/port2008/
