Main menu
Nahajate se tukaj
Optimizacija geometrije prostih površin
Optimizacija geometrije prostih površin
Simon Kulovec, Leon Kos in Jožef Duhovnik
Laboratorij za računalniško podprto konstruiranje - LECAD
Fakulteta za strojništvo
Univerza v Ljubljani
LECAD je razvil specializirani CAD modelirnik z vgrajeno paralelno optimizacijo geometrije fasad posplošenih oblik in tvorjenjem različnih rešitev vozlišč. Dele konstrukcije lahko izvozimo v splošne modelirnike in tam podrobneje analiziramo.
Na slikah vidimo modelirnik s katerim lahko interaktivno optimiziramo izhodiščno mrežo na želeno končno obliko s podajanjem uteži različnim cenilkam in hkrati upoštevamo omejitve geometrije kot je planarnost ploskev ali koničnost vozlišč. Z optimiziranjem dobimo želeno obliko in hkrati dobimo tudi ravnost ploskev, kar lahko sproti analiziramo. Zaradi unikatnosti vseh elementov strukture je izdelan generator CAD geometrije v kateri lahko neposredno preverjamo različne koncepte geometrije vozlišč in optimizacijo pod-konstrukcije. Celoto ali izbrane dele lahko nato izvozimo v standardne modelirnike za nadaljno analizo in preračune.
Geometrija za arhitekturo prostih oblik zahteva preverbo različnih aspektov v virtualnem okolju pred samo realizacijo projekta. Zasnova nepravilnih oblik, ki jih predvidi arhitekt vsebuje posebne zahteve za računsko geometrijo, ki jih je mogoče izpolniti z optimizacijo geometrije. Ta geometrija je tako zahtevna, da je potrebna tesna povezava med mrežnim modelom in parametričnim tvorjenjem strukture v CAD jedru saj so vsi tvorjeni deli strukture unikatni. Projekt predstavlja tako povezavo med mrežo in CAD jedrom. Uporaba hiterarhične zasnove z izborom stopnje podrobnosti omogoča prenos v druga CAD-CAM orodja za implementacijo in nadaljnjo analizo.
Za optimizacijo se zaradi želje po hitrejšem reševanju matrik, ki v realnih aplikacijah vsebujejo veliko ničelnih elementov, uporabi PARDISO solver, ki računa z stisnjenega zapisom redkih matrik. PARDISO solver je hiter in spominsko učinkoviit Uporablja se za reševanje velikih redkih (sparse) simetričnih in nesimetričnih linearnih sistemov z uporabo večih procesorjev. Formati zapisa redkih matrik, ki jih uporablja PARDISO solver so zapisani na način, da se iz matrik prebere in kasneje operira samo z neničelnimi elementi. Obstaja več vrst formatov zapisa redkih matrik ampak vsi formati temeljijo na podobnih osnovah. To je shranjevanje vseh neničelnih elementov v linearne vektorje in uporaba pomožnih vektorjev, ki opisujejo lokacijo posameznega neničelnega elementa v originalni matriki. V našem primeru uporabljamo CSR način formatiranja, kar pomeni, da neničelne elemente matrike, ki zapisujemo v enodimenzijski vektor beremo zaporedno po vrsticah.
Glede na optimizirane vrednosti koordinat posameznega vozlišča in uporabo CAD jedra se izdela CAD model različnih konceptov konstrukcij. Izdela se lahko knstrukcijo iz delnih, posameznega ali celotne optimizirane mreže. CAD model se lahko, preko standardnih formatov za pronos CAD modelov (npr. STEP, IGES,...), izvozi v ostale modelirnike, kjer se lahko izdela tudi trdnostna analiza.

Slika 1: Uporaba redkih matrik (sparse matrix) v obliki CSR.
V večini primerov realnih aplikacij iskanja rešitev je večina elementov matrike A enaka nič. Zapis take matrike je možno zmanjšati in tako vrsto matrike imenujemo redka matrika (sparse matrix). Izračun rešitve Ax = B za redke matrike je možno izvesti veliko bolj učinkovito s strani časovnega in spominskega vidika, v primeru da lahko dosežemo redkost matrike, ki jo obravnavamo.
Formati zapisov redkih matrik (Sparse Matrix Storage Formats)
Spominski format redkih matrik je učinkovitejši, ker deluje na principu shranjevanja samo neničelnih elementov v redko matriko. Obstaja več vrst formatov zapisa redkih matrik ampak vsi formati temeljijo na podobnih osnovah. To je shranjevanje vseh neničelnih elementov v linearne vektorje in uporaba pomožnih vektorjev, ki opisujejo lokacijo posameznega neničelnega elementa v originalni matriki.
Shranjevanje neničelnih elementov redke matrike v linearni vektor se izvede tako, da se premikamo zaporedno po posameznem stolpcu (column-major ali CSC format) ali po posamezni vrstici (row-major ali CSR format). Vrednosti redke matrike zapisujemo po vrsti, glede na potek branja redke matrike, v linearne vektorje. Za simetrične matrike je pomembno, da shranimo samo zgornji trikotni del matrike (upper triangular format) ali spodnji trikotni del matrike (lower triangular format).
Za popis in reševanje posamezne redke matrike se uporabi tri vektorje: values, columns and rowIndex. Kjer vektor values vsebuje zaporedne neničelne vrednosti redke matrike, vektor columns vsebuje mesto na katerem se nahajajo zaporedno prebrane neničelne vrednosti redke matrike. Zadnji vektor rowIndex, pa vsebuje število neničelnih elementov, ki se pojavijo v posamezni vrstici oz. stolpcu. Dolžina posameznega vektorjev values and columns je enaka številu neničelnih elementov matrike. Vektor rowIndex nam poda lokacijo prvega neničelnega elementa v posamezni vrstice. oz stolpcu (odvisno ali uporabljamo CSR ali CSC formatiranje) in vsebuje rowIndex[i+1] - rowIndex[i] elementov v posamezni vrstice oz. stolpcu. Če od števila vseh elementov, ki jih vsebuje vektor rowIndex odštejemo ena dobimo število stolpcev oz. vrstic matrike. Glede na zapisovanje mest in štetje elementov elementov se uporablja štetje, ki se začne z ena ali nič. Predvsem je pomembno, da se en tip štetja uporabi skozi celoten postopek reševanja redke matrike.
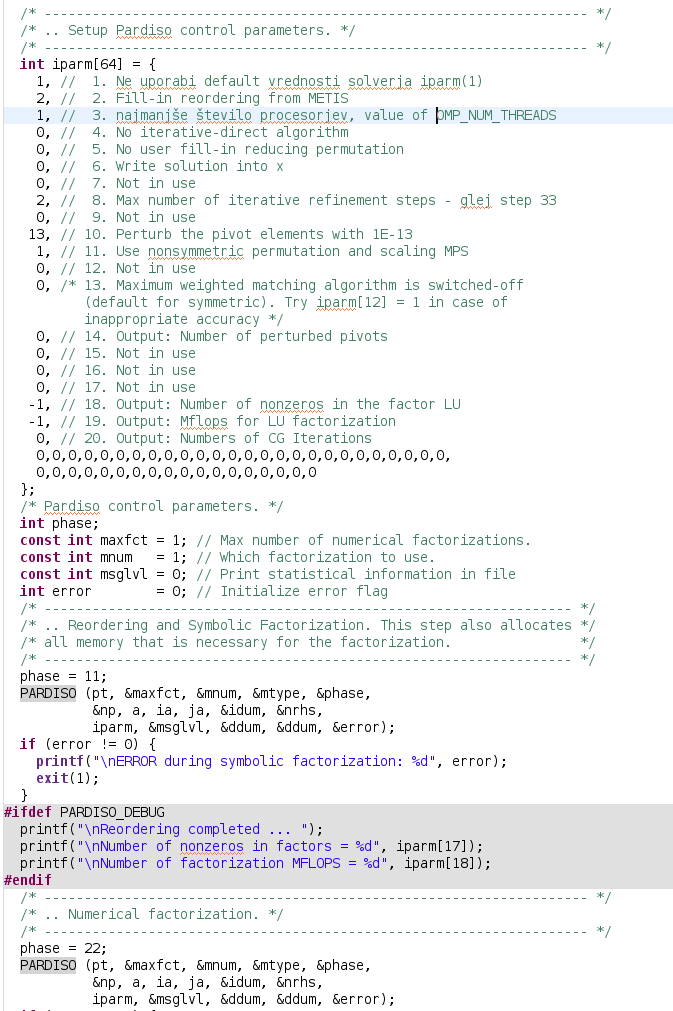
Slika 2: Uporaba "paralelnega direktnega solverja" (PARDISO solver) v rutini za optimizacijo geometrije.
"Paralelni direktni solver" PARDISO solver je visoko zmogljiv, hiter, robusten, spominsko učinkovit in enostaven za uporabo. Uporablja se za reševanje velikih redkih (sparse) simetričnih in nesimetričnih linearnih sistemov z uporabo večih procesorjev. Solver uporablja LR drevesno razporejanje (left- and right-looking) z Level-3 BLAS (angl. Basic Linear Algebra Subprograms) večvozliščno tehniko. Level-3 BLAS tehnika omogoča osnovno linearno algebro in sicer operacije med matrikami [Schenk00-2]. Za izboljšanje sekvenčnih in paralelnih redkostnih numeričnih razcepnih lastnosti, se uporablja algoritme na osnovi Level-3 BLAS in vzporednosti s kombinacijo z LR drevesnega razcepa (left- and right-looking) z večvozliščno tehniko [Schenk00, Schenk01, Schenk02, Schenk03]. Metode paralelnega pivotiranja omogočajo celostno večvozliščno pivotiranje, za zagotovitev numerične stabilnosti in skalabilnosti tekom procesa razcepa (factorization process).
PARDISO solver podpira široko območje različnih tipov redkih matrik (sparse matrix) in izračuna rešitve realnih ali kompleksnih, simetričnih, strukturno simetričnih ali nesimetričnih, pozitivno definitnih, nedefinitnih ali Hermitian redkih linearnih sistemov enačb na več procesorski arhitekturi.
PARDISO izračuna rešitev seta večih redkih linearnih enačb
A*X = B
z različnimi metodami, ki uporabljajo paralelni LU, LDL ali LLT razcep, kjer je A matrika velikosti [n x n] ter X in B sta vektorja velikosti [n]. PARDISO solver uporablja format redkih matrik (Sparse Matrix Storage format).
PARDISO solver opravlja štiri naloge:
- analiza in simbolični razcep,
- numerični razcep,
- zamenjavo spredaj in zadaj (forward and backward substitution) z upoštevanjem iterativnega izpolnjevanja,
- prenehanje in sprostitev internega spomina solverja.
Manipulacija mrežnih struktur z uporabo programa Tremesh
V arhitekturi se pojavlja trend izdelovanja mrežnih konstrukcij prostih oblik. Tehnologija mreženja je bila fundamentalno namenjena in razvita za mreženje elementov predvsem v avtomobilski in letalski industriji. V našem primeru, pa želimo tehnologijo mrežnih konstrukcij uporabiti za arhitekturne aplikacije, ki se v kar nekaj stvareh razlikujejo od elementov, za katere je bila tehnologija razvita. Razlike so predvsem v estetiki, statiki, velikosti mrež in postopku izdelave končnega izdelka oz. konstrukcije. Predvsem se pojavijo problemi, ker vizualizacijska orodja za upravljanje s takimi vrstami konstrukcij ne obstajajo. Za konstrukcijo posledično ne moremo izdelati CAD modela s katerim se lahko preveri pravilnost konstrukcije in možne napake. Zato izdelava prosto površinskih (angl. freeform) konstrukcij predstavlja izziv med obliko in izdelavo konstrukcije. Načeloma bi lahko prosto površinske konstrukcije uvrstili, kot novo raziskovalno področje arhitekturne geometrije (angl. Architectural Geometry), katero je prvič omenil Pottmann. Ugotovljeno je bilo, da se z uporabo geometrijske optimizacije lahko izdela mrežno strukturo, ki zadošča vsem pogojem izdelave. Glavni cilj raziskave je izdelava optimizacijskega algoritma za poljubne mrežne strukture. Algoritem naj iz nepravilne mrežne strukture izdela mrežno strukturo, ki ustreza vsem kriterijem izdelave konstrukcije. Za izdelavo strukture lahko uporabimo trikotno ali štirikotno mrežno strukturo.
Zaradi želje po zmanjšanju stroškov s strani izdelovalnega vidika se odločimo za poglobitev izdelave programa za manipulacijo predvsem z štirikotniškimi mrežnimi strukturami. Porabimo manjše število sestavnih pokrivnih elementov in nosilcev. Lažje je povezovanje nosilnih elementov pri štirikotni mrežni strukturi. Zato se naša raziskava usmerja predvsem v analizo štirikotne mrežne strukture, čeprav programski algoritem pokriva tudi ostale n-kotne mreže. Potrebno pa je paziti tudi na posebne mrežne elemente, ki se pojavijo v mreži. Kot posebni mreži element npr. obravnavamo pojav tri ali pet kotnega mrežnega elementa v štirikotni mrežni strukturi.
Cilj razvoja algoritma in implementacija le tega v samostojni program Tremesh je zmanjšati ekonomske, izdelovalne in stroške s strani časa izvedbe konstrukcije. Želimo omogočiti štirikotno mrežno strukturo za poljubno vhodno obliko konstrukcije. Za omenjeno je potrebno vhodno mrežno strukturo optimizirati glede na planarnost, izbočenost (koničnost), glavne ukrivljenosti itd.

Slika 3: Uporabniški vmesnik programa Tremesh in prikaz uvoza enostavne mrežne strukture, ki se jo lahko ureja z orodji prikazanimi pod zavihkom Urejanje.
Gostitev mreže z delitvijo (Subdivider)
Optimizacija na koničnost vozlišč je zahtevna omejitev, ki potrebuje za stabilno konvergenco izhodiščno mrežo v bližini končnega modela. Eden od postopkov, ki zagotavlja tvorjenje primerne mreže, je iteracija v kateri se iz grobega modela mreže postopoma gosti mrežo tako, da se jo deli v manjše dele. Pri tem se ohranjajo tvornice in osnova mreže (angl. design intent). Končna mreža je gladka in ima enakomerne velikosti elementov. Vse to je pomembna lastnost pri konstruiranju fasad amorfnih oblik.
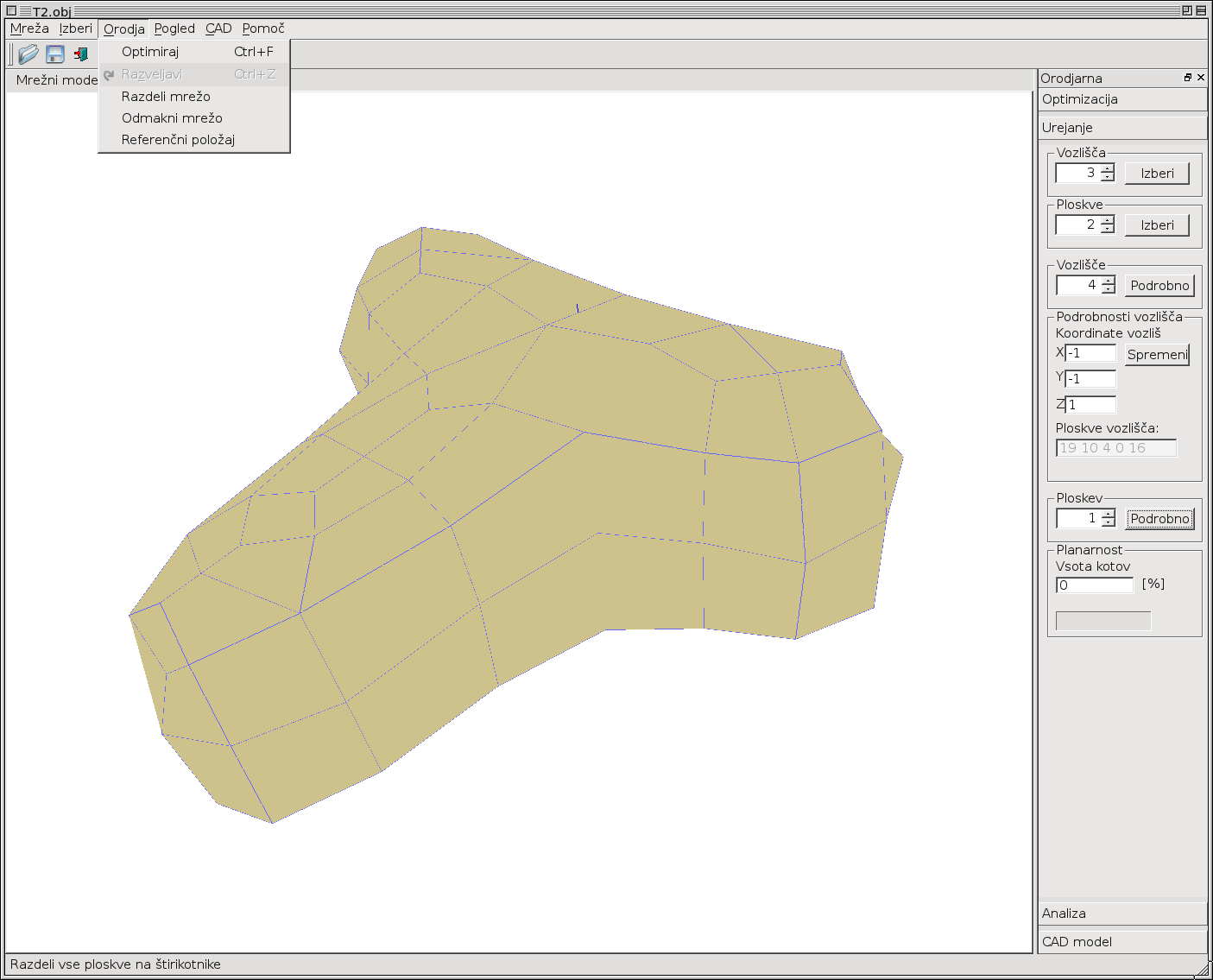
Slika 4: Uporabniški vmesnik programa Tremesh in prikaz funkcije za delitev mreže s pomočjo Catmull-Clark algoritmu (Orodja/Razdeli mrežo)
Za štirikotniške mreže obstajata naslednja algoritma:
- Catmull-Clark
- Doo-Sabin
Razdelitev na štirikotniško mrežo je najprimernejša metoda za fabrikacijo. V Tremesh je vgrajena metoda Catmull-Clark delitve, ki z vsakim klicem v meniju Orodja/Razdeli mrežo funkcija enkrat razdeli mrežo. Metoda Catmull-Clark delitve je splošna, kar pomeni tudi, da trikotnike deli na štirikotnike in je zato končna mreža vedno štirikotniška.
V nadaljevanju je prikazana delitev mreže z uporabo Catmull-Clark algoritma.
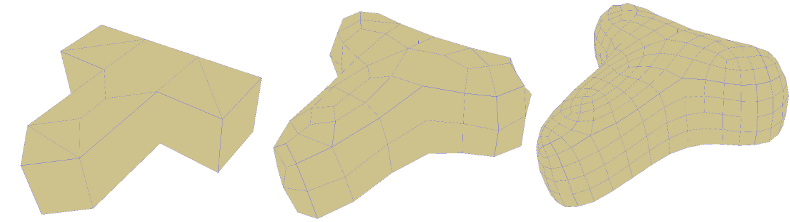
Slika 5: Osnovni model (levo), model z enkratno Catmull-Clark delitvijo (sredina) in dvakratna Catmull-Clark delitev modela (desno).
Optimizacija položaja vozlišč (Perturber)
V praksi obstaja več vrst optimiziranja za omejeni linearni problem. Vse metode lahko uvrstimo v dve večji skupini: posredne in neposredne metode. Obe metodi temeljita na osnovi iterativnega iskanja vektorja rešitve X, za minimalno vrednost cenilne funkcije pri enakostnih in neenakostnih omejitvenih pogojih: in . Pri direktnih metodah so omejitve optimizacijskega problema upoštevane eksplicitno. V primeru neposrednih metod optimiziranja se omejitveni problem rešuje kot set večih zaporednih neomejenih problemov. Dani geometrijski optimizacijski problem rešujemo s pomočjo neposrednih nelinearnih tehnik optimiziranja. Za reševanje se izbere metoda sekvenčnega kvadratičnega optimiziranja (angl. Sequential Quadratic Optimization - SQO), ki temelji na metodi kvadratičnega optimiziranja.
Sekvenčno kvadratično programiranje (angl. Sequential Quadratic Programming - SQO) je ena izmed najboljših optimizacijskih metod. Metodo teoretično lahko razdelimo na dva dela: (1) reševanje seta nelinearnih enačb z uporabo Newtonove metode in (2) z uporabo Kuhn-Tuckerjevih pogojev Lagrangeove funkcije omejitvenega optimizacijskega problema. SQO je iterativna metoda, kar pomeni, da se išče rešitev optimizacijskega problema po korakih.
V prejšnjem odstavku smo formulirali problem lokalnega minimuma omejene funkcije z iskanjem stacionarne točke Lagrangeove funkcije. V nadaljevanju za iskanje optimalne rešitve formuliranega problema uporabimo metodo: (i) sekvenčno kvadratične optimizacije (SQO) ali (ii) Lagrange Newtonovo optimizacijo (angl. The Lagrange Newton Optimization Method – LNM). Metodi SQO in LNM se v nekaterih korakih iskanja rešitev razlikujeta. Razlike dajejo prednosti metodi LNM posebno pri pisanju računalniških optimizacijskih algoritmov. Prva prednost LNM se kaže pri linijskem iskanju (angl. soft line search) z uporabo posebne vrste kaznovalne funkcije (angl. penalty function). Drugi del LNM se od SQO razlikuje po načinu izračuna Hessianove matrike (angl. Update method for the Hessian matrix). Zaradi omenjenih dveh sprememb LNM imenujemo Quasi-Newton-ova metoda z dobro končno (angl. super linear convergence) konvergenco in pri LNM ne potrebujemo računati drugih odvodov.
Perturber omogoča premikanje vozlišč v prostoru s ciljem zadovoljevanja kriterijev planarnosti, koničnosti in drugih optimizacijskih zahtev. Topologija mreže se pri optimizaciji ne spreminja.

Slika 6: Optimizacijske funkcije programa Tremesh.
Pred vsako optimizacijo je potrebno nastaviti največje število korakov. Če se globalni kriterij optimizacije ustavi prej, se optimizacija samodejno (predčasno) ustavi in statusno okno napiše Optimizacija ponovno na voljo.
Optimizacija poteka v ločeni niti (thread) in tako omogoča uporabniku, da med samim potekom opazuje konvergenco planarnosti in koničnosti. Privzeta možnost animacije se lahko med optimizacijo na željo uporabnika tudi izključi, kar nekoliko pospeši samo optimizacijo na eno-procesorskih računalnikih.
Optimizacijo lahko tudi kadarkoli prekinemo z gumbom Prekini. Le ta počaka, da se zadnji korak dokonča. Po tem koraku se lahko parametri optimizacije spremenijo in ponovno uporabijo.
Analiza mrežnega modela
Planarnost štirikotniških vozlišč: V Perturber-ju se za optimizacijo planarnosti uporablja, za inženirsko oceno najbolj primerna, ocena, ki v dolžinskih enotah predstavlja odstopanje od ravnine. Ta mera je za prikaz vgrajena v Tremesh.
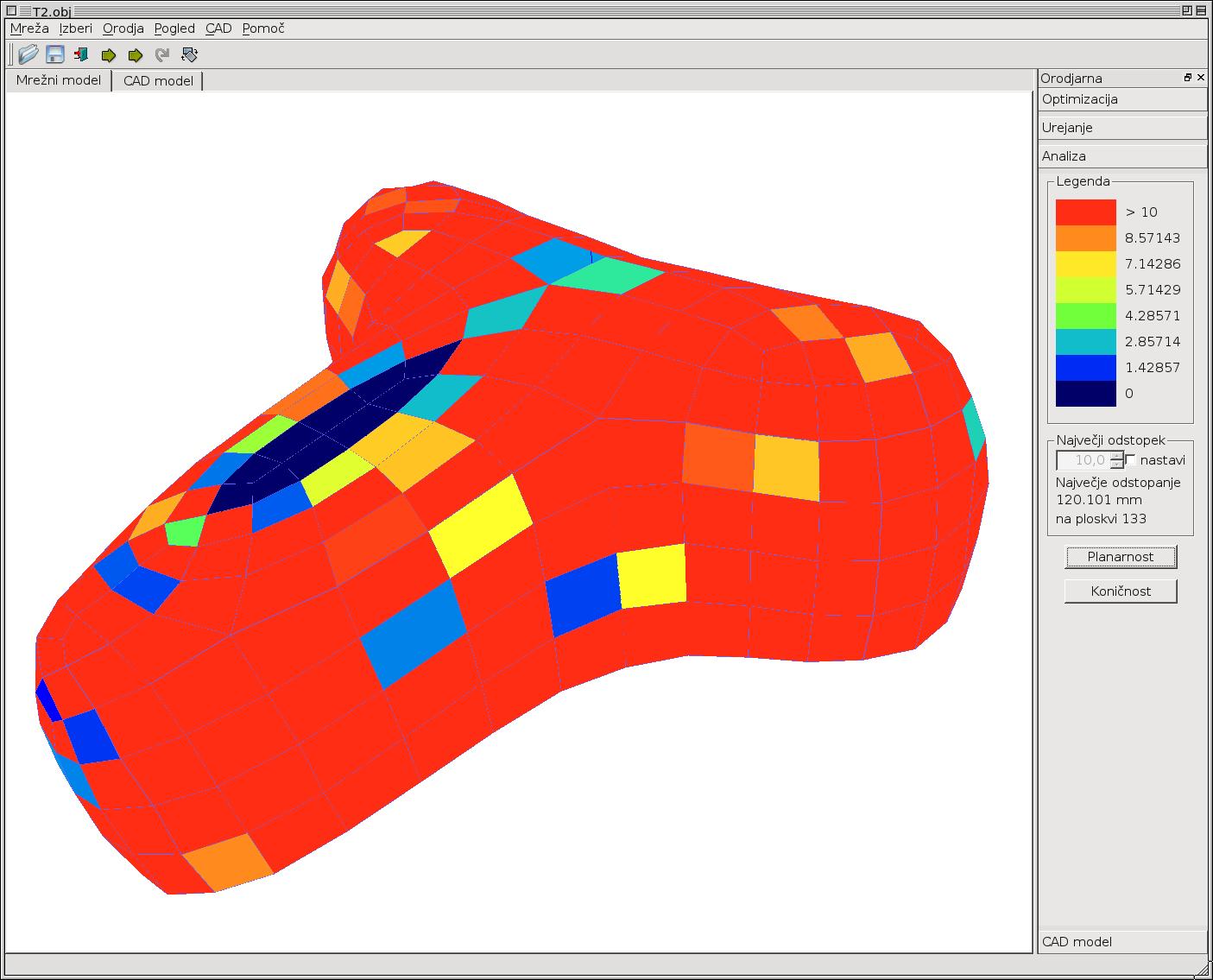
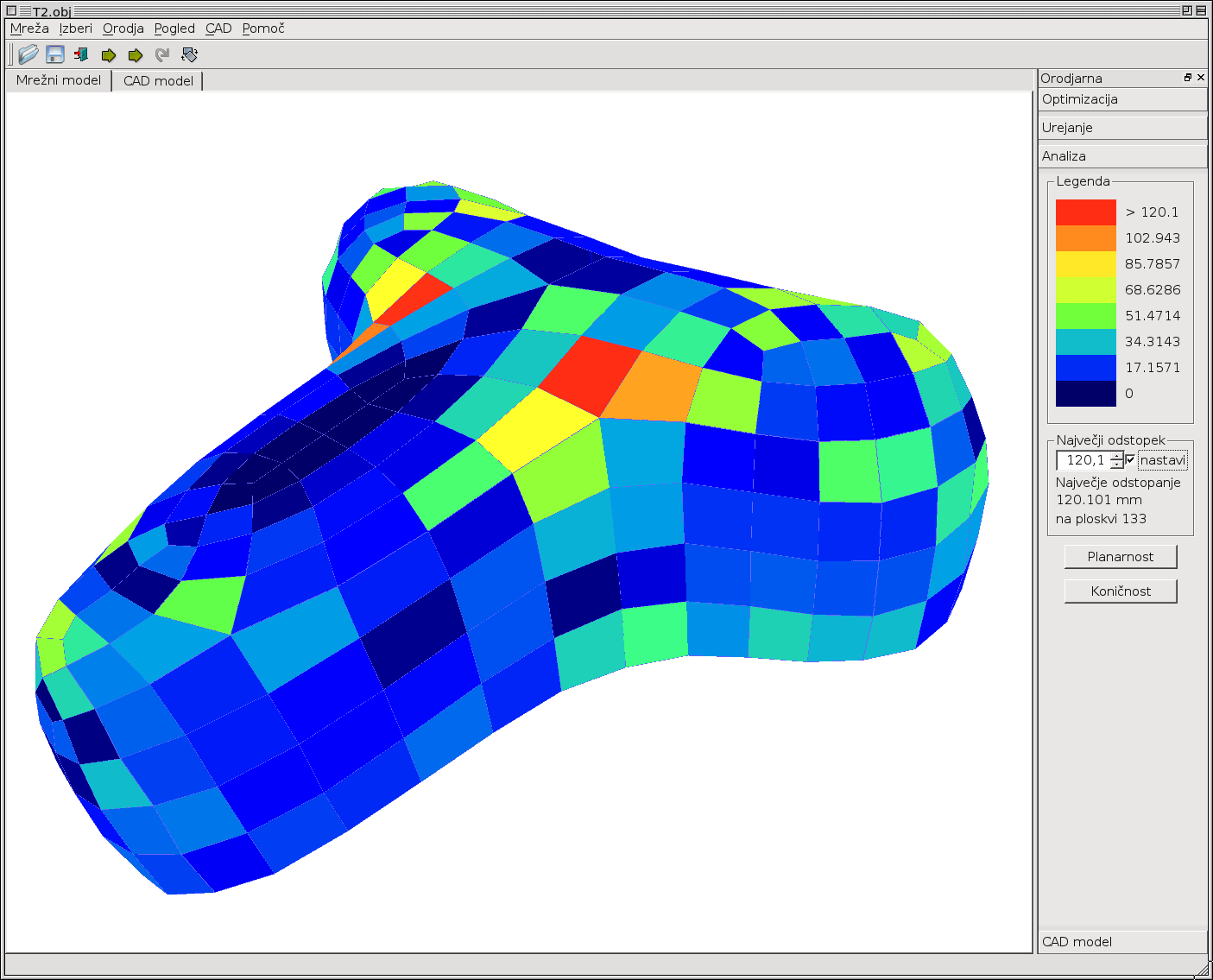
Slika 7: Legenda planarnosti fiksirana na 10mm (levo) in legenda planarnosti nastavljena relativno glede na maksimalno odstopanje, ki se pojavi na mreži (desno).
Izbočenost (koničnost) štirikotniških vozlišč: Z izbočenostjo vozlišč pojmujemo lastnost vozlišča, da tvori odmične površine (offset surface) v točki. Če so vsa vozlišča mreže izbočena, je možno izdelati odmično površino s konstantnim odmikom in enako povezljivostjo mreže. V primeru da kakšno vozlišče ni izbočeno, se običajno izkaže, da presek ploskev v vozlišču ni več točka ampak je linija. Možne pa so tudi druge degeneracije vozlišča. Izbočenost posameznega vozlišča izražamo v mrad.
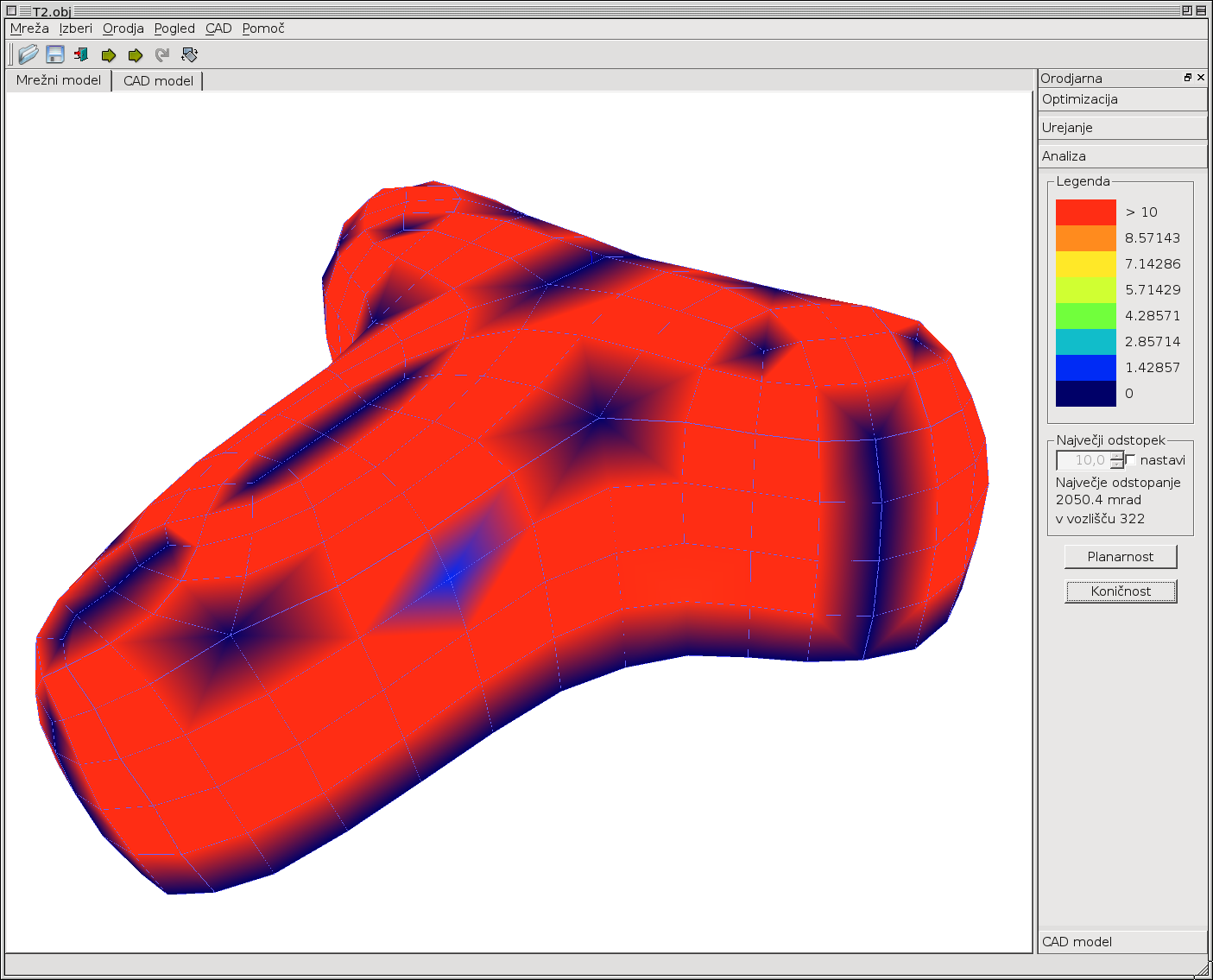
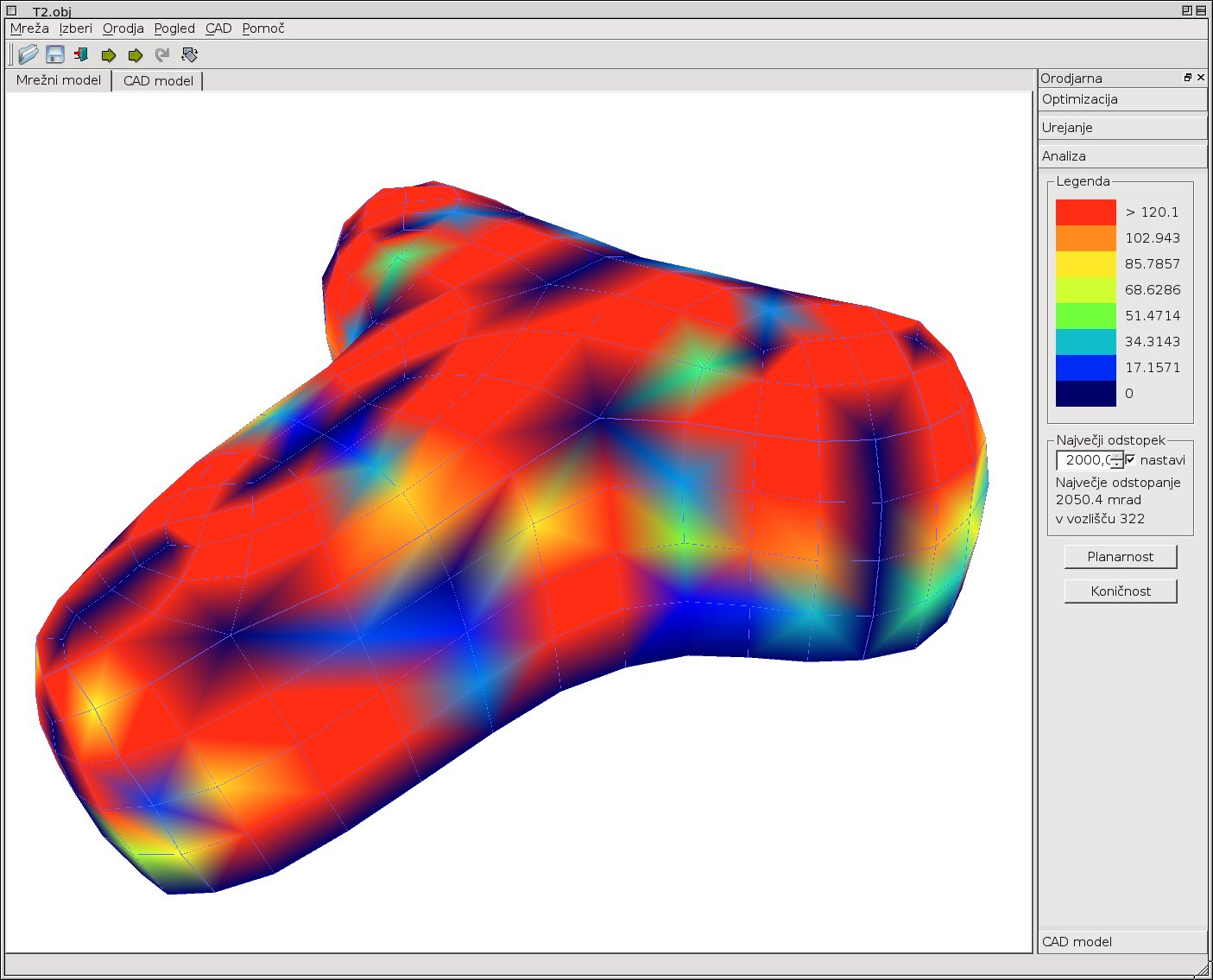
Slika 8: Legenda izbočenosti (koničnosti) fiksirana na 10mrad (levo) in legenda izbočenosti nastavljena relativno glede na maksimalno odstopanje, ki se pojavi na mreži (desno).
Nastavitev legende planarnosti in izbočenosti (koničnosti) je možna v relativnem, kot tudi absolutnem smislu z uporabo kontrolnega okenčka nastavi, ki samodejno nastavi zgornjo mejo na trenutno največje odstopanje. Če je ta kontrolnik stalno vključen, je prikaz relativen. Sicer pa lahko z dva kratnim zagonom ukaza za planarnost oz. izbočenost enkratno nastavimo najvišjo vrednost v mreži, in nato kažemo odstopanje v absolutnem smislu.
Primeri animacij optimizacij
Naslednji primeri optimizacij glede na planarnost so bili izvedeni na standardni PC opremi s programom Tremesh. V kasnejših različicah se je večkratno pospešila optimizacija, tako da so časi optimizacij informativne narave. Optimizacija je bila izvedena brez cenilke Baricenter, ki preferira štirikotnike enakostranične štirikotnike.
Vse slike optimizacij mreže so izdelane kot animacije v obliki animirane slike v formatu GIF.
Enostavni štirikotni mrežni model - Cubes:
- 30 korakov
- največje začetno odstopanje 434,7 mm
- rdeča barva označuje odstopanje > 10mm
- velikost diagonale 3 m
- končno odstopanje 0.0033 mm
- čas optimizacije 5 sekund

Slika 9: Animacija enostavnega štirikotnega mrežnega modela.
Štirikotni mrežni model - Tcc2:
- 100 korakov
- največje začetno odstopanje 120,1 mm
- rdeča barva označuje odstopanje > 10mm
- velikost diagonale 1.5 m
- končno odstopanje 0.91 mm
- čas optimizacije 6 minut

Slika 10: Kompleksnejši štirikotni mrežni model, dobljen z dvojno Catmull-Clark delitvijo začetne mreže.
Štirikotni mrežni model - Fig7cc2:
- 200 korakov
- največje začetno odstopanje 196 mm
- rdeča barva označuje odstopanje > 10mm
- velikost diagonale 0.7 m
- končno odstopanje 0.6 mm
- čas optimizacije 14 minut

Slika 11: Kompleksnejši štirikotni mrežni model z večimi odprtimami, dobljen z dvojno Catmull-Clark delitvijo začetne mreže.
Izdelava CAD modela za izvoz v STEP ali IGES format
V arhitekturi se pojavlja želja po prostih oblikah fasad. Ker z preverjanjem konceptov v modelirnikih lahko še pred izdelavo ugotovimo možne težave pri sestavljanju izhodiščne mrežne sestave je potrebno obstoječo mrežno strukturo poljubnega modela, ki jo generiramo z programom Tremesh pretvoriti v končni CAD model. Izhodiščno mrežo pretvorimo v končni model tako, da avtomatsko generiramo znane detajle elementov (pokrivna pločevina, tesnilni element, robni nosilec, izolacija, ...). Druga uporabna vrednost parametričnega modela je generiranje detajlov za statične analize strukture (izdelava ustrezne abstrakcijo vseh spojev za FEM analize). Za vse omenjene namene je potreben CAD model, katerega lahko uvozimo v poljuben modelirnik. Standardna formata datotek, podprta v večini modelirnikov sta STEP in IGES. Za modeliranje geometrije se uporabi CAD jedro (odprtokodno CAD jedro OpenCascade), ki omogoča zahtevne operacije na geometriji. V modulu Cad model je uporabljeno odprtokodno CAD jedro Open Cascade (Matra Datavision).
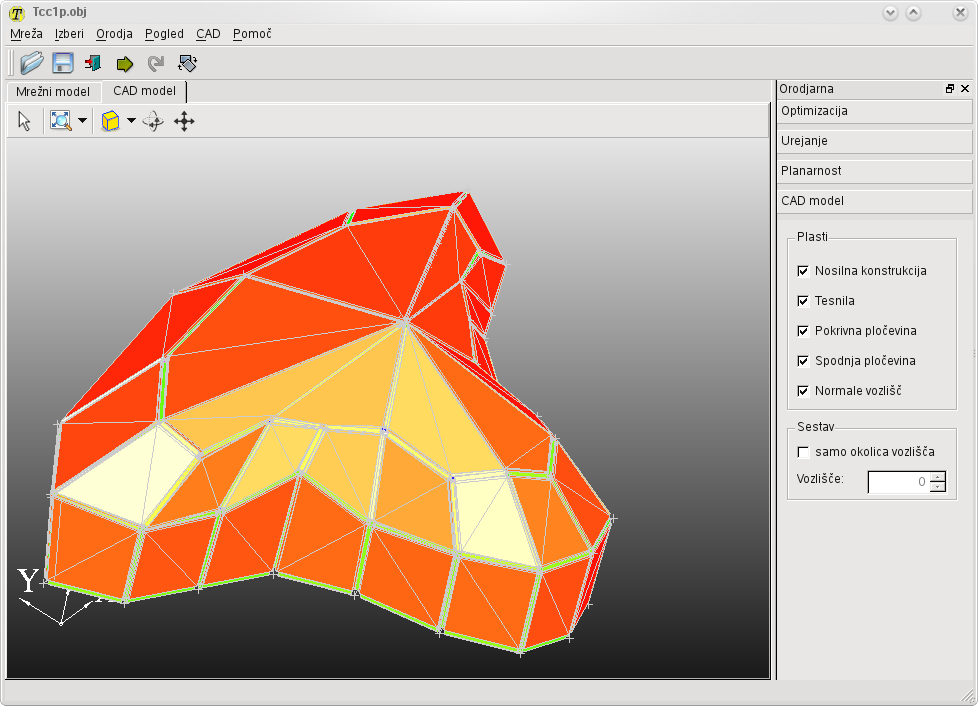
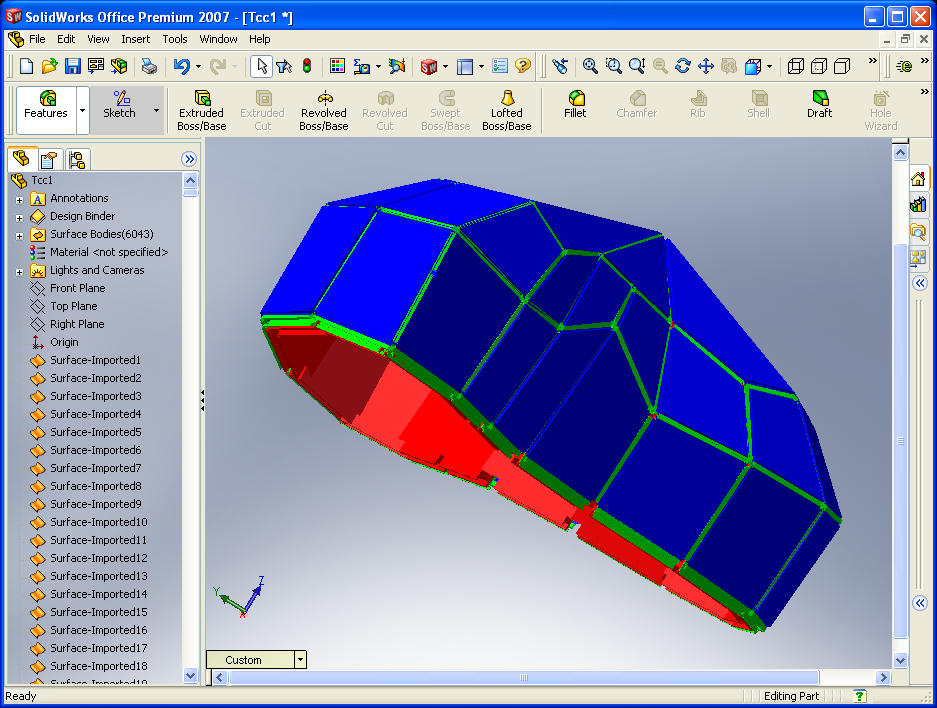
Slika 12: Avtomatsko generirani CAD model z uporabo odprtokodnega CAD jedra OpenCascade (levo) in prikaz uvoza STEP datoteke, generirane s programom Tremesh, v komericialni program SolidWorks 2007 (desno).
Modul CAD v programu Tremesh omogoča izdelavo CAD modelov rszličnih sklopov konstrukcije. Prikazane sklope je mogoče izvoziti v STWEP ali IGES formatu, posamezno ali kot celoto. Prikazan je tudi uvoz, z OpenCascade tvorjene, STEP ali IGES datoteke v komercialni modelirnik SoliWorks 2007.
Nagrade
Za odličnost diplomskega dela je bila Simonu Kulovcu podeljena nagrada Trimo Research Award 2010.

Bibliografija
- KULOVEC, Simon, DUHOVNIK Jože. Parametrični model konične vozliščne strukture prostih oblik fasad, 2009, diplomsko delo, [COBISS.SI-ID 11045403]
- KULOVEC, Simon, DUHOVNIK Jože. Modeliranje vozliščne strukture prostih fasadnih oblik, 2009, prešernova nagrada, [COBISS.SI-ID 11264539]
- KOS, Leon, KULOVEC, Simon, ZALETELJ, Viktor, DUHOVNIK, Jože. Structure generation for free-form architectural design. Advanced engineering, 2009, vol. 3, no. 2, str. 187-194, ilustr. [COBISS.SI-ID 11096091]
- KOS, Leon, KULOVEC, Simon, ZALETELJ, Viktor, DUHOVNIK, Jože. Parametric CAD model for free-form architectural design. V: OBSIEGER, Boris (ur.). 7th International Conference on Computer Aided Design and Manufacturing, September 22nd-26th 2009, Hvar, Croatia. CADAM 2009 : proceedings. Rijeka: Zigo, 2009, str. 31-32, ilustr. [COBISS.SI-ID 11091995]
- KOS, Leon, KULOVEC, Simon, DUHOVNIK, Jože, SUPPORT STRUCTURE OPTIMIZATION FOR FREEFORM ARCHITECTURAL DESIGN, TMCE 2010 [COBISS.SI-ID 11371547]
| Priponka | Velikost |
|---|---|
| 66.68 KB | |
| 106.04 KB | |
| 61.16 KB | |
| 85.23 KB | |
| 89.98 KB | |
| 81.53 KB | |
| 303.38 KB | |
| 218.23 KB | |
| 72.08 KB | |
| 9.03 KB | |
| 12.5 KB | |
| 17.34 KB | |
| 73.7 KB | |
| 300.14 KB | |
| 69.99 KB | |
| 1.65 MB | |
| 5.24 MB | |
| 17.95 KB | |
| 41.33 KB |
