- Predstavitev
- Uporaba
- Projekti in dogodki
- European HPC Summit Week 2018
- International HPC Summer School 2016
- Kampus šola HPC 2014
- PRACE Autumn School 2013
- PRACE Autumn school 2018
- PRACE Autumn school 2020
- PRACE Summer of HPC 2014
- PRACE Summer of HPC 2015
- PRACE Summer of HPC 2016
- PRACE Summer of HPC 2017
- PRACE Summer of HPC 2018
- PRACE Summer of HPC 2019
- PRACE Summer of HPC 2020
- PRACE campus in poletna šola HPC
- Po kreativni poti - Superračunalnik za vse
- Poletna delavnica 2021
- Poletna delavnica HPC 2014
- Poletna delavnica HPC 2015
- Poletna delavnica HPC 2016
- Poletna delavnica HPC 2017
- Poletna delavnica HPC 2018
- Poletna delavnica HPC 2019
- Poletna delavnica HPC 2020
- Poziv za PRACE TIER-0
- Poziv za predloge ARRS 2012 projektov računsko intenzivnih simulacij
- Poziv za predloge projektov računsko intenzivnih simulacij
- Poziv za simulacije ANSYS
- Projekta EUFORIA in EFDA-ITM-ISIP
- Summer of HPC 2013
- Numerical Simulation of the Turbolent Flow around the Sphere
- Optimizacija geometrije prostih površin
- Razširitev nekolizijskih razelektritvenih modelov za aplikacijo v fuzijsko relavantnih in splošnih plazmah
- Velocity profile effects in coriolis mass flowmeters
- Numerične simulacije na področju varnosti cestnih in terenskih vozil
- CDF modeling of breathing process influence on personal exposure effectiveness
- Rotating cascade heat transfer using CFD and IR thermography
- Simulating the dynamics of clapper-to-bell impact
- Strateški raziskovalno-razvojni projekt
- Parallel computing with load balancing
- Laser droplet generation datachment regimes
- Prijava
- Wiki
Main menu
Nahajate se tukaj
Vaje za Kampus šolo
MPI
Pri vajah na HPC bodo razložene osnove uporabe in računanja na HPC ter osnove MPI v jeziku C.
Spodaj so opisane vse vaje, skupaj z izvorno kodo (le-ta je tudi v priponkah na dnu strani). Pozor pri kodi – spletni urejevalnik ne mara kombinacij znakov ‘<’ in ‘>’, zato pri vseh ‘#include’ direktivah manjka začetni ‘<’. Sicer pa se v priponkah nahaja popolna koda. Prevajanje posameznih programov z ukazom mpicc -std=c99 -O3 ime_programa.c -o ime_programa poganjanje pa nato z ukazom mpirun -n stevilo_procesov ime_programa parametri_programa, kjer označen tekst primerno nadomestimo.
Vaja1
Prva vaja zajema spodaj prikazano začetno programsko kodo, ki uporablja MPI, ali tako imenovani “Hello World!” v jeziku C z uporabo MPI. V kodi sta pomembna dva sklopa ukazov, ki skrbita za uspostavitev povezave med procesi, ki se lahko poženejo na fizično ločenih računalnikih. Pri MPIju se namreč običajno vsi procesi ustvarijo iz istega izvedljivega programa. Požene jih MPI okolje v nastavljivem številu, na podanih računalnikih ter na tak način, da se bodo kasneje znali identificirati in komunicirati med seboj.
Prvi sklop zajema funkciji MPI_Init in MPI_Finalize, ki se vedno kličeta v paru in skrbita za povezavo programa z okoljem MPI. MPI_Init vzame kot parametre kar kazalce na parametre, ki so podani main funkciji programa, to sta argc in argv. Veliko MPI implementacij namreč uspostavi povezavo med procesi s pomočjo argumentov programu v ukazni vrstici. MPI_Init argumente prebere, in izloči vse njemu namenjene iz spremenljivg argc in argv, tako da jih program po klicu MPI_Init ne vidi več.
Drugi sklop zajema funkciji MPI_Comm_rank in MPI_Comm_size. Kot večina ostalih funkcij, se morata ti dve funkciji klicati po klicu MPI_Init in pred klicem MPI_Finalize. Ti dve funkciji skrbita za to, da se vsak proces lahko identificira znotraj skupine procesov, ki sestavljajo en MPI program. Prva funkcija povpraša MPI okolje po identifikacijski številki oziroma ranku znotraj MPI skupine procesov (MPI_COMM_WORLD), ki je dobila dovoljenje za medsebojno komunikacijo. Vsak od procesov dobi od MPIja drug rank, ki je predstavljen kot celo število na intervalu od 0 do n, kjer je n število vseh procesov. Po številu n vsak proces vpraša MPI preko funkcije MPI_Comm_size.
Konstanta MPI_COMM_WORLD, ki se uporablja pri pridobitvi ranka in števila vseh procesorjev pognanih prek MPI, definira tako imenovani komunikator. Komunikator je objekt znotraj MPI okolja, ki definira skupino procesov z uspostavljenimi kanali za medsebojno komunikacijo. Zato sta pridobljeni vrednosti rank in število procesorjev veljavni le znotraj podanega komunikatorja. Poleg tega definira tudi kako se sporočajo napake pri komunikaciji in pri klicih MPI funkcij. Privzeti komunikator, ki zajema vse procese, ki jih je MPI ustvaril ob zagonu programa je določen kar s konstanto MPI_COMM_WORLD, sicer pa je možno dodatne komunikatorje z bolj omejenimi skupinami procesov ustvariti tekom programa.
Zadnji MPI ukaz, ki se uporablja v spodnjem primeru, je MPI_Get_processor_name. Za delovanje programa je to povsem nepomemben ukaz, pomaga pa identificirati računalnik, na katerem posamezen proces teče.
#include mpi.h>
#include stdio.h>
int main(int argc, char **argv) {
int rank, size;
char name[MPI_MAX_PROCESSOR_NAME];
int sLen;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
MPI_Get_processor_name(name, &sLen);
printf("%s is rank %d of %d\n", name, rank, size);
MPI_Finalize();
}
Vaja2
Druga vaja izhaja iz prve in jo razširi z osnovnima gradnikoma komunikacije med dvema procesoma (peer to peer).
Nova je uporaba funkcij MPI_Send (pošlji sporočilo) in MPI_Recv (sprejmi sporočilo). Sporočilo je v MPI izraženo kar kot spremenljivka, ki je lahko enostavnega tipa, npr int, double, char, tabelaričnega tipa, npr: int[10], float* ali pa sestavljenega tipa, torej strukture. Na teh vajah bodo uporabljene le spremenljivke osnovnih tipov in tabelarične. Funkciji sprejmeta naslednjih 5 oziroma 6 parametrov v podanem vrstnem redu:
- void* buffer je kazalec na pomnilnik v katerem se nahaja sporočilo, ki ga želi proces poslati ali pa pomnilnik kamor naj se shrani sporočilo, ki ga želi proces sprejeti.
- int length podaja število osnovnih enot, v katerih je izražena velikost spremenljivke buffer.
- MPI_Datatype type podaja tip osnovne enote, v podanem primeru je to MPI_INT - konstanta, ki označuje tip “int" v jeziku C. prvi trije parametri skupaj definirajo spremenljivko, ki predstavlja sporočilo, oziroma prostor, kamor naj se zapiše sporočilo.
- int src/dest je rank procesa od kogar se sprejema ozirma kamor se pošilja sporočilo.
- int tag je oznaka sporočila. S pomočjo oznak je možno sporočila klasificirati in filtrirati.
- int comm je ročaj (handle) na komunikator. proces s katerim želimo komunicirati je enolično dolečen preko kombinacije parametrov src/dest in comm.
- MPI_Status* status je parameter MPI_Recv funkcije, kamor le-ta zapiše nekaj dodatnih informacij o prejetem sporočilu. MPI_Send tega parametra ne vsebuje.
V spodnjem programu vsi procesi pošljejo in sprejmejo po eno sporočilo. Proces p pošlje sporočilo procesu p+1 po modulu n in ga prejme od procesa p-1 po modulu n; n je število vseh procesov. Oznaka (tag) sporočila mora biti enaka pri pošiljanju in sprejemanju, sicer pa njena vrednost ni pomembna. MPI ne pregleduje če je sporočilo istega tipa pri pošiljanju in sprejemanju, sporočilo se namreč med transportom spremeni v niz bajtov in informacija o njegovem tipu se ne ohranja. MPI preveri le, da je podana spremenljivka buffer pri sprejemanju dovolj velika, da vanjo shrani celotno sporočilo. Če ni, potem spremenljivko napolni do konca, ostanek sporočila pa vrže proč. Pri sprejemu bi lahko zapisali napačen tip ali pa napačno velikost, kar bi povzročilo napačen sprejem, oziroma napačno interpretacijo sprejetega sporočila. Ne bi pa dobili nobenega opozorila glede tega, ne od prevajalnika, ne od MPI okolja v izvajanju.
#include mpi.h>
#include stdio.h>
int main(int argc, char **argv) {
int rank, size;
int source, dest, tag=0xf00d;
int sendBuf, recvBuf;
MPI_Status status;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
source = (rank - 1) % size;
dest = (rank + 1) % size;
sendBuf = 10*rank;
recvBuf = 0;
MPI_Send (&sendBuf, 1, MPI_INT, dest, tag, MPI_COMM_WORLD);
MPI_Recv (&recvBuf, 1, MPI_INT, source, tag, MPI_COMM_WORLD, &status);
printf("Process %3i sent %5i and received %5i\n", rank, sendBuf, recvBuf);
MPI_Finalize();
}
Zgornja koda je na žalost le na pol pravilna oziroma nevarna za uporabo, vključuje namreč zadostne pogoje za nastanek zastoja (deadlock). Vsi procesi namreč najprej pošljejo sporočilo nato pa ga sprejemjo. Če bi bilo sporočilo daljše - koliko daljše je odvisno od implementacije - bi MPI_Sand blokiral izvajanje. Zakaj? Zato ker se pošiljanje sporočila ne more izvesti, če na drugi strani nihče ne pričakuje sporočila in zanj ni pripravil mesta v pomnilniku. MPI_Sand zato v primeru, ko ne more poslati sporočila čaka da proces na drugi strani kliče MPI_Recv, šele nato pošlje celotno sporočilo in zaključi. Zgornja koda pa na kratkih sporočilih (kratko je tudi uporabljeno - le en int) vseeno deluje, saj se kratka sporočila lahko shranijo znotraj MPI okolja, na primer kar v pomnilniku mrežne kartice.
Vaja3
Tretja vaja prikazuje en način preprečitve zastoja - z uporabo neblokirajočih funkcij. Izvorno kodo druge vaje najprej spremenimo tako, da procesi pošiljajo in sprejemajo tabelo števil namesto enega samega števila. Velikost tabele je shranjena v novi spremenljivki length, spremenljivki sendBuf in recvBuf pa postaneta tabeli dinamične velikosti, ki ju kasneje alociramo z ukazom malloc. Kodo spremenimo tako da vključuje napisane spremenljivke, po vzorcu spodaj, vendar MPI funkcije pustimo še nedotaknjene. S spreminjanjem velikosti tabele (s spremenljivko length) lahko vidimo pri kateri velikosti se bo zgodil zastoj (program bo takrat treba ubiti z tipkama ctrl+c)
Da odpravimo zastoj nadaljujemo s spreminjanjem kode, tokrat z MPI funkcijami. Najprej popravimo spremenljivko status, ki postane tabela dolžine 2. Tabela mora biti zato, da jo lahko podamo funkciji MPI_Waitall, njena dolžina pa se mora ujemati z dolžino naslednje spremenljivke. To je spremenljivka request, ki je tabela tipa MPI_Request, dolžine 2 in predstavlja dva ročaja na objekta, ki se zgradita ob klicu dveh neblokirajočih funkcij. Neblokirajoči funkciji MPI_Isend in MPI_Irecv sta podobni njunima osnovnima različicama (MPI_Send in MPI_Recv), le da vključujeta nov parameter, parametra status pa ne uporabljata več. Nov parameter je spremenljivka tipa MPI_Request, ki jo podamo preko kazalec in ki naj bo ob uporabi neinitializirana ali pa že sproščena (ne smemo je 'reciklirati' tako da bi na primer obema funkcijama podali isto). Po klicu neblokirajoče funkcije bo podana spremenljivka tipa MPI_Request dobila za vsebino veljaven ročaj na objekt, ki v MPIju predstavlja zahtevek po komunikaciji. Ta objekt sprostimo z klicem funkcije MPI_Wait, ali v našem primeru, ko imamo tabelo spremanljivk, z ukazom MPI_Waitall. Slednji sprejme kot parametre velikost obeh tabel, tabelo MPI_Request spremenljivk in tabelo MPI_Status spremenljivk. Ukaz je blokirajoč in se zaključi šele, ko se vsi podani zahtevki za komunikacijo sprostijo, to je, ko se zahtevane komunikacije zaključijo. Po tem klicu lahko tabelo request recikliramo za naslednjo komunikacijo, v tabeli status pa dobimo rezultat komunikacije - podobno kot ga vrne MPI_Recv. Trenutno nas statusi še ne zanimajo, zato jih ignoriramo.
Po vseh spremembah deluje spodnja koda vedno brez zastojev, ne glede na velikost tabele, ki jo pošiljamo.
#include mpi.h>
#include stdio.h>
#include stdlib.h>
int main(int argc, char **argv) {
int rank, size;
int source, dest, tag=0xf00d;
int *sendBuf, *recvBuf, length = 10000;
MPI_Status status[2];
MPI_Request request[2];
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
source = (rank - 1) % size;
dest = (rank + 1) % size;
sendBuf = malloc(length * sizeof(int));
recvBuf = malloc(length * sizeof(int));
sendBuf[0] = 10*rank;
recvBuf[0] = 0;
MPI_Irecv(recvBuf, length, MPI_INT, source, tag, MPI_COMM_WORLD, &request[0]);
MPI_Isend(sendBuf, length, MPI_INT, dest, tag, MPI_COMM_WORLD, &request[1]);
MPI_Waitall(2, request, status);
printf("Process %3i sent %5i and received %5i\n", rank, sendBuf[0], recvBuf[0]);
free(sendBuf);
free(recvBuf);
MPI_Finalize();
}
Druga pogosto uporabljena rešitev za odpravljanje zastojev se izogne uporabi neblokirajočih funkcij z preureditvijo njihovega vrstnega reda.
Vaja4
V četrti vaji izhajamo iz druge vaje in spremenimo vrstni red pošiljanja sporočil pri enem samem procesu. Najprej pa popravimo spremenljivko, ki vsebuje sporočilo. Podobno kot v prejšnji vaji naredimo iz nje tabelo, a tokrat le eno: buf. Ne pozabimo na malloc in free ko gre za dinamično alocirano tabelo!
Kako enemu procesu spremenimo izvajanje? Z testiranjem njegovega ranka. Z if stavkom ločimo kodo, ki naj jo izvaja proces z rankom 0 od kode, ki naj jo izvajajo ostali. V kodi za proces 0 zapišemo ukaza MPI_Send in MPI_Recv v istem zaporedju, kot sta bila uporabljena že prej, v kodi za ostale procese pa zamenjamo njun vrstni red. Tako je program preoblikovan v obliko kjer ne more priti do zastoja. Izvršil se bo namreč takole: proces 0 bo poslal sporočilo procesu 1 proces 1 bo prejel sporočilo od procesa 0, ga spremenil in poslal procesu 2 proces 2 bo prejel sporočilo od procesa 1, ga spremenil in poslal procesu 3 ... proces n-1 bo prejel sporočilo od procesa n-2, ga spremenil in poslal procesu 0 proces 0 bo prejel sporočilo in izpisal preštel število 'skokov' sporočila.
V programu poljubno nastavimo začetno sporočilo in spreminjanje sporočila na vsakem skoku. V spodnjem primeru je narejeno podobno kot v vaji 2, le da je dodano še štetje skokov, ki se akumulira v prvem elementu sporočila.
#include mpi.h>
#include stdio.h>
int main(int argc, char **argv) {
int rank, size;
int source, dest, tag=0xf00d;
int *buf, length = 10000; // length naj bo vsaj 2
MPI_Status status;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
source = (rank - 1) % size;
dest = (rank + 1) % size;
buf = malloc(length * sizeof(int));
if (rank == 0) {
buf[0] = 1;
buf[1] = 10*rank;
MPI_Send(buf, length, MPI_INT, dest, tag, MPI_COMM_WORLD);
MPI_Recv(buf, length, MPI_INT, source, tag, MPI_COMM_WORLD, &status);
printf("Process %3i sent %5i and received %5i\n", rank, 10*rank, buf[1]);
printf("The result of the count = %i\n", buf[0]);
} else {
MPI_Recv(buf, length, MPI_INT, source, tag, MPI_COMM_WORLD, &status);
printf("Process %3i received %5i and sent %5i\n", rank, buf[1], 10*rank);
buf[0] += 1;
buf[1] = 10*rank;
MPI_Send(buf, length, MPI_INT, dest, tag, MPI_COMM_WORLD);
}
free(buf);
MPI_Finalize();
}
Zgornja vaja sicer uspešno odpravlja mesto, kjer lahko nepreviden programer naredi hudo napako, a ne naredi vzporednega programa, temveč le zaporedni program, katerega posamezni bloki se izvajajo v različnih procesih. Preden začnemo z zares vzporednimi programi, še malo popravimo četrto vajo in se ustavimo še pri enem posebnem MPI ukazu, ki se lahko izvede tudi pred MPI_Init in po MPI_Finalize.
Vaja5
Peta vaja seznani z merjenjem časa v MPI. Spodnja koda pomeri razliko v času, ki ga javljajo različni procesi. Že po občutku verjetno lahko vidimo, da se četrta vaja izvaja kar dolgo, vsekakor dlje kot bi se ekvivalenten zaporeden program (štetje do n, kjer je n majhna številka). Pri razvoju vzporednih programov pa je zelo koristno, če občutek nadomestimo z resno meritvijo, ki da konkretne odgovore na vprašanje kateri program je najhitrejši in koliko je hitrejši od ostalih. MPI daje na razpolago funkcijo MPI_Wtime, ki vrne število sekund od neke fiksne točke v preteklosti. Kaj je ta točka v preteklosti ni definirano in nas niti ne zanima. MPI_Wtime se uporablja v paru, rezultata pa se odšteje, tako da se dobi razliko v času med prvim in drugim klicem.
Prejšnjo vajo spet predelamo. Dodamo nekaj spremenljivk tipa double (timeStamp, timeStart, timeEnd, minCommTime, timeOffset) v katerih bomo hranili posamezne meritve časa. Predelamo tudi dela kode za proces 0 in ostale procesorje. Pri obeh delih se spremenita velikost in tip sporočila (1, MPI_DOUBLE) ter spremenljivka ki hrani sporočilo (timeStamp). V kodi za proces 0 dodamo klica funkcije MPI_Wtime takoj pred in takoj po komunikaciji. Ti dve meritvi bosta služili le prepoznavanju natančnosti meritve. V delu kode za ostale procese dodamo meritev časa (timeStamp = MPI_Wtime();) takoj za MPI_Recv in pred MPI_Send. Da bi dobili boljšo meritev dodamo spremenljivko repeats in ji določimo razmeroma nizko vrednost. V obeh delih kode dodamo še zanko, tako da se komunikacija in vse meritve časa ponovijo repeats-krat. V delu kode za proces 0 dodamo še eno zanko, ki do nastavljala cilj komunikacije (tokrat poimenovan p) od 1 do size. Tako preoblikovan proces 0 bo izmenično pošiljal komuniciral z vsemi posameznimi procesi. Tudi v delu kode za ostale procese popravimo izvor/cilj komunikacije na 0, ker ne bodo več komunicirali med seboj ampak le še z procesom 0. Dodamo še del kode, ki shrani razliko med časom na p-tem procesu in procesu 0 takrat, ko se komunikacija zgodi najhitreje. Ta del kode v kombinaciji z ponavljanjem komunikacije poskrbi za to, da bo rezultat izmerjen ob najbolj ugodnem trenutku in ne takrat, ko bodo kaki dogodki iz ozadja upočasnili kateregakoli od sodelujočih procesov. Na koncu naročimo procesu 0 da izpiše izmerjeno razlilko v času v milisekundah (timeOffset*1000)
Program lahko še izboljšamo z dodatnim klicom MPI_Get_processor_name, in sporočanjem prebranega imena procesu 0 takoj po koncu zanke z merjenjem razlike v časih. Sporočanje izvedemo prek MPI_Send in sprejmemo v procesu 0 prek MPI_Recv, z spremenljivko name za sporočilo. Za lažjo orientacijo dodamo še izpis resolucije (najmanjšega možnega izmerjenega časa) časovnika (timer), ki ga uporablja MPI.
Če poženemo spodnji program na več procesih enega računalnika bomo zelo verjetno dobili razliko v časih enako 0 zaradi slabe natančnosti časovnika (na POSIX sistemih naj bi bila resolucija 1 mikrosekunda). Če ga poženemo porazdeljenega na več računalnikov pa bodo razlike v časih postale bolj zanimive. Malo se bodo povečale že zato, ker bo že komunikacija dodala nekaj časa. Še več pa se lahko povečajo zaradi razlike v sistemskih urah na različnih računalnikih. Sistemska ura je sicer pogosto sinhronizirana na posameznih vozliščih superračunalnikov a kljub temu lahko vedno pričakujemo odstopanja vsaj v rangu nekaj mikrosekund.
#include mpi.h>
#include stdio.h>
int main(int argc, char **argv) {
int rank, size, sLen;
char name[MPI_MAX_PROCESSOR_NAME], otherName[MPI_MAX_PROCESSOR_NAME];
int tag=0xf00d, repeats=1000;
double timeStamp, timeStart, timeEnd, minCommTime, timeOffset;
MPI_Status status;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
MPI_Get_processor_name(name, &sLen);
if (rank == 0) {
for (int p = 1; p < size; ++p) {
for (int i = 0; i < repeats; ++i) {
timeStart = MPI_Wtime();
MPI_Send(&timeStamp, 1, MPI_DOUBLE, p, tag, MPI_COMM_WORLD);
MPI_Recv(&timeStamp, 1, MPI_DOUBLE, p, tag, MPI_COMM_WORLD, &status);
timeEnd = MPI_Wtime();
if ((i == 0) || (timeEnd - timeStart < minCommTime)) {
minCommTime = timeEnd - timeStart;
timeOffset = timeEnd - timeStamp;
}
}
MPI_Recv(otherName, MPI_MAX_PROCESSOR_NAME, MPI_CHAR, p, tag, MPI_COMM_WORLD, &status);
printf("Time offset between %s and %s: %f ms\n", name, otherName, timeOffset*1000);
printf("(Timer resolution is %f ms\n", MPI_Wtick()*1000);
}
} else {
for (int i = 0; i < repeats; ++i) {
MPI_Recv(&timeStamp, 1, MPI_DOUBLE, 0, tag, MPI_COMM_WORLD, &status);
timeStamp = MPI_Wtime();
MPI_Send(&timeStamp, 1, MPI_DOUBLE, 0, tag, MPI_COMM_WORLD);
}
MPI_Send(name, MPI_MAX_PROCESSOR_NAME, MPI_CHAR, 0, tag, MPI_COMM_WORLD);
}
MPI_Finalize();
}
Vaja6
Program iz pete vaje (nehote) že meri naslednjo zanimivo lastnost komunikacije prek MPI. To je čas za prenost sporočila. Šesta vaja zato izepljuje peto v obliko, ki namesto razlike v časovnikih procesorjev, ugotavlja čas porabljen za en 'ping' sporočila.
Spodnja koda je že rezultat brisanja odvečnih spremenljivk in odvečne kode. Glavne spremembe v primerjavi s peto vajo so v tem, da se je sporočilo spet spremenilo v tabelo, da se čas prenosa meri le še v procesu 0 in da se je merjenje premaknilo ven iz najožje zanke. Sedaj torej merimo čas zanke v kateri se repeat-krat ponovi komunikacija z procesom p. Ta čas nato delimo z številom ponovitev ter z 2 (sporočilo potuje do drugega procesa in nazaj, torej je 2x v prenosu) in dobimo čas za prenos enega sporočila prej nastavljene velikosti. Poračunamo lahko še pasovno širino (koliko bajtov ana sekundo zmoremo prenesti). Če predelamo program še tako, da lahko dolžino sporočila nastavljamo od zunaj, preko parametra podanega programu, lahko enostavno preverimo razliko v hitrosti komunikacije s sporočili različne dolžine.
#include mpi.h>
#include stdio.h>
#include stdlib.h>
int main(int argc, char **argv) {
int rank, size, sLen;
char name[MPI_MAX_PROCESSOR_NAME], otherName[MPI_MAX_PROCESSOR_NAME];
int tag=0xf00d, repeats, msgSize, total = 10000000;
double timeStart, timeEnd;
MPI_Status status;
char* buffer;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
MPI_Get_processor_name(name, &sLen);
if (argc > 1)
msgSize = atoi(argv[1]);
else
msgSize = 200;
if (msgSize > total)
msgSize = total;
repeats = total/msgSize;
buffer = malloc(total);
if (rank == 0) {
for (int p = 1; p < size; ++p) {
printf("Communicating with process %d\n", p);
timeStart = MPI_Wtime();
for (int i = 0; i < repeats; ++i) {
MPI_Send(buffer+i*msgSize, msgSize, MPI_CHAR, size-1, tag, MPI_COMM_WORLD);
MPI_Recv(buffer+i*msgSize, msgSize, MPI_CHAR, size-1, tag, MPI_COMM_WORLD, &status);
}
timeEnd = MPI_Wtime();
MPI_Recv(otherName, MPI_MAX_PROCESSOR_NAME, MPI_CHAR, p, tag, MPI_COMM_WORLD, &status);
printf("Measurements for message size of %d bytes transferred between %s and %s: transfer time = %f ms; bandwidth = %f MB/s\n", msgSize, name, otherName, (timeEnd - timeStart)*1000/(2*repeats), (2*total/1000000)/(timeEnd - timeStart));
}
} else if (rank == size-1) {
for (int i = 0; i < repeats; ++i) {
MPI_Recv(buffer+i*msgSize, msgSize, MPI_CHAR, 0, tag, MPI_COMM_WORLD, &status);
MPI_Send(buffer+i*msgSize, msgSize, MPI_CHAR, 0, tag, MPI_COMM_WORLD);
}
MPI_Send(name, MPI_MAX_PROCESSOR_NAME, MPI_CHAR, 0, tag, MPI_COMM_WORLD);
}
free(buffer);
MPI_Finalize();
}
Spodnja grafa sta narisana iz rezultatov poganjanja programa iz vaje 6 na dveh računalnikih, povezanih z 1GB Ethernet povezavo. Poganjanje je bilo izvedeno v zanki:
for (( n=2; n<10000000; n=n*2 )); do mpirun -n 2 -hostfile hosts ./Vaja6 $n; done
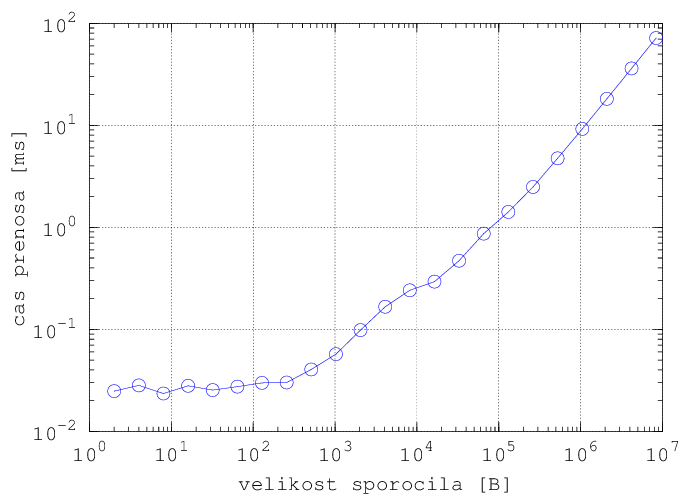
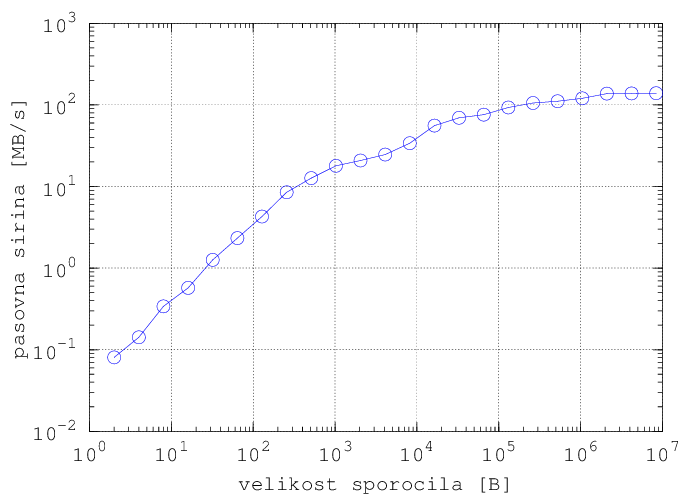
Dobro referenco za vse uporabljene MPI ukaze predstavljajo dokumenti, ki jih ponuja MPICH: http://www.mpich.org/static/docs/v3.1/
Sicer pa je najboljša referenca kar MPI forum:
http://www.mpi-forum.org/docs/docs.html
Še vedno dober ‘plonk listek’ za najbolj pogoste MPI ukaze se nahaja na:
http://web.eecs.utk.edu/~dongarra/WEB-PAGES/SPRING-2006/mpi-quick-ref.pdf
OpenMP
Drugi del vaj predstavlja osnove OpenMP. Vaje so narejene tako, da iz prejšnje vaje sledi naslednja (po številki). Večinoma gre za dodatne vrstice v programu, redko se zgodi večji ‘reset’ programske kode.
Kodo za spodnje vaje se prevaja z gcc -fopenmp -std=c99 -O3 ime_fajla.c -o ime_programa in nato zažene z ./ime_programa Za razliko od MPI torej OpenMP nima svojega izvajalnega okolja in se pravilno izvaja znotraj operacijskega sistema. Ni niti potrebna uporaba knjižnic ali posebnega postopka za prevajanja, le stikalo/zastavica -fopenmp pove prevajalniku, da uporabljamo tudi OpenMP. V drugih prevajalnikih je ta zastavica lahko drugačna, sicer je pa povsod tako, da je OpenMP implementiran kot del prevajalnika in ne kot zunanje okolje.
Vaja1
“Hello world” z OpenMP. Vaja prikazuje osnovni razvoj programa v vzporedni program. OpenMP okolje je zelo enostavno za nastavit, pravzaprav je sestavljeno iz enega include-a in ene #pragma direktive. Pragma direktiva poskrbi, da se celoten blok (scope) izvede vzporedno, na n-nitih, kjer je n definiran kot sistemska spremenljivka znotraj operacijskega sistema OMP_NUM_THREADS, ali kot število jeder, ki ga detektira OpenMP, ali pa znotraj programa podano število.
Število jeder lahko znotraj programa podamo na dva načina, in sicer z funkcijo omp_set_num_threads(n), ki velja za vse prihodnje omp pragme, ter kar znotraj pragme, z dodanim num_threads(n).
Vaja2 in Vaja3
Kako iz osnovnega programa pridemo do programa ekvivalentnega prvim programom v MPI okolju. Program prikazuje razdelitev po nitih (ekvivalentno procesom pri MPI). Dodatna ukaza sta omp_get_thread_num() in omp_get_num_threads(). Pri pragma direktivi je novo deklariran ‘private (id)‘ v Vaji 2, pri Vaji 3 pa je namerno izpuščen. Deklaracija private(spremenljivka1, spremenljivka2, ...) pove OpenMP kodi, da mora podane spremenljivke narediti ločene za vsako nit – vsaka nit torej vidi svojo verzijo iste spremenljivke. Sicer so te spremenljivke ‘globalne’ in vse niti vidijo isto verzijo spremenljivke. Zakaj deklariramo nekatere spremenljivke kot private? Zato, ker ne sme več niti hkrati brati in pisati po istem prostoru v pomnilniku – le to ni varno in lahko pripelje do napačnih rezultatov oziroma v skrajenm primeru celo do obešanja programa.
Vaja4
Skupinsko delo niti na isti spremenljivki. Če vsaka nit dela na svojem delu spremenljivke (na primer tabele ali niza znakov, kot v vaji), potem lahko do spremenljivke dostopajo brez skrbi. Spremenljivka mora ostati definirana kot globalna (k omp pragmi ne smemo dodati deklaracija private (sillyString)).
Na tem mestu je treba povedati, da private deklaracija ne kopira vrednosti spremenljivke. Ko vsaka nit dobi svojo spremnljivko, je vrednost le-te povsem nedefinirana. Smatra se torej, da bo programer vanjo nekaj zapisal in ne bral iz nje. Prav tako se sklepa, da programer ne bo želel njene vrednosti ohranjati po končanju vzporednega bloka. Katero vrednost bi sploh ohranil, če pa ima vsaka nit svojo spremenljivko? Zato obstaja razširitev firstprivate, ki nadomešča private, kadar želimo, da je začetna vrednost spremenljivke initializirana kar iz globalne spremenljivke z istim imenom. Ekvivalentno temu je tudi lastprivate, ki naredi obratno – končno vrednost lokalne spremenljivke iz niti ki zadnja konča izvajanje vzporednega dela skopira v globalno spremenljivko.
#include stdio.h>
#include omp.h>
int main (int argc, char **argv) {
int id, numThreads;
char sillyString[100] = " [oooooooooooooooooooooooooooooo] <- tu je 30 o-jev ";
printf("This is the main thread of the program\n");
printf("Silly string = '%s'\n", sillyString);
#pragma omp parallel private(id)
{
id = omp_get_thread_num();
numThreads = omp_get_num_threads();
printf("This is thread #%d of %d\n", id, numThreads);
sillyString[2 + id] = (char)('0'+id);
}
printf("back to the main thread\n");
printf("Silly string = '%s'\n", sillyString);
}
Vaja5
Največkrat uporabljen vzporedni konstrukt pri OpenMPju je vzporedna for zanka. Kako jo napišemo vidimo v vaji 5. Od vaje 4 je spremenjena pragma deklaracija in for zanka takoj za njo. Znotraj vzporednega bloka tudi zakomentiramo izpis id-ja niti, da ne smetimo po zaslonu. Rezultat tega programa bo niz znakov, v katerem bo vsak znak predstavljal zaporedno številko niti, ki ga bo nastavila. Po rezultatu poganjanja vidimo, da si niti med seboj razdelijo približno enako velike kose zanke in sicer kar po vrsti. Prva nit dobi začetek zanke v izračun, druga nit dobi drugi kos, itd do zadnje niti, ki dobi v izračun zadnji kos zanke.
#include stdio.h>
#include omp.h>
int main (int argc, char **argv) {
int id, numThreads;
char sillyString[100] = " [oooooooooooooooooooooooooooooo] <- tu je 30 o-jev ";
printf("This is the main thread of the program\n");
printf("Silly string = '%s'\n", sillyString);
#pragma omp parallel for private(id)
for (int i = 0; i < 30; ++i) {
id = omp_get_thread_num();
numThreads = omp_get_num_threads();
// printf("This is thread #%d of %d\n", id, numThreads);
sillyString[2 + i] = (char)('0'+id);;
}
printf("back to the main thread\n");
printf("Silly string = '%s'\n", sillyString);
}
Vaja6
V tej vaji povečamo obseg dela posamezne niti. Tako kot prej si nit zapiše svoj id v niz znakov, ki ga preimenujemo v threads. Poleg tega pa še zapiše rezultat svojega dela v niz znakov results. Njeno delo pa je preverjanje števila za deljivost – iskanje praštevila. Kot vhod je podano zaporedje velikih števil, tako da morajo niti opraviti neko netrivialno delo. Preiskovanje teh števil nato opravimo z vzporedno zanko. Testiranje števil za praštevila je postopek, katerega trajanje je močno odvisno od števila. Število deljivo s 3 naprimer bo preverjeno in zavrnjeno kot praštevilo že v prvi iteraciji funkcije isPrime, medtem ko bodo praštevila potrebovala približno 5 milionov korakov, da bodo preverjena do konca. Zato je v zanki, ki testira 60 števil, zelo neenakomerno porazdeljeno delo in bi običajma razdelitev na niti lahko povzročila slabo učinkovitost programa.
Zato dodamo novo specifikacijo: schedule(dynamic) v pragma omp deklaraciji, ki naroči prevajalniku, da naj ne razdeli zanke med niti že vnaprej (vsaki en del), ampak naj iteracije sproti dodeljuje med proste niti. Algoritem porazdeljevanja niti lahko nastavimo tudi na druge načine, vse zapišemo v deklaracijo schedule. Privzeti način je static (ki ga lahko preizkusimo v tem primeru da vidimo razliko), drugi najbolj pomemben pa je tu uporabljeni dynamic.
#include stdio.h>
#include omp.h>
#include stdbool.h>
bool isPrime(long n) {
if ((n & 1) == 0)
return false;
for (long i=3; i*i <= n; i += 2)
if ((n % i) == 0)
return false;
return true;
}
int main (int argc, char **argv) {
int id, numThreads;
char results[200] = "[------------------------------------------------------------]";
char threads[200] = "[------------------------------------------------------------]";
long numbers[100];
printf("results = %s\n”, results);
printf("threads = %s\n”, threads);
for (int i = 0; i < 100; ++i)
numbers[i] = 100000000000001l + 2*i;
#pragma omp parallel for private(id) schedule(dynamic)
for (int i = 0; i < 60; ++i) {
id = omp_get_thread_num();
numThreads = omp_get_num_threads();
results[1 + i] = (isPrime(numbers[i]) ? '1' : ‘0');
threads[1 + i] = (char)(id + '0');
}
printf("results = %s\n”, results);
printf("threads = %s\n”, threads);
}
Vaja7
V tej vaji dodamo še štetje praštevil. Vsaka nit naj poveča števec praštevil za 1, kadar najde praštevilo. Prej smo že omenili, da se globalnih spremenljivk ne sme nezaščiteno spreminjati znotraj niti. Kako torej varno povečevati globalno spremenljivko count? Ker gre za enostavno spremenljivko (= spremenljivko osnovnega tipa) in za enostavno operacijo (prištevanje 1, oziroma inkrement), imamo na izbiro vewč možnosti, od katerih je najboljša ta, ki je prikazana v tej vaji. Omp pragmi dodamo deklaracijo reduction(+: count). Ta nam povzroči dve stvari. Najprej razdeli spremenljivko count med nitmi, podobno kot to stori ukaz private(count). Vse niti zato varno štejejo z uporabo te lokalne spremenljivke. Ko niti končajo svoje delo, OpenMP sešteje vse vrednosti lokalnih spremenljivk count in rezultat zapiše v globalno spremenljivko count. Vse skupaj zato iz programerskega stališča spet izgleda enako, kot če bi uporabljal navadno (sekvenčno) for zanko.
#include stdio.h>
#include omp.h>
#include stdbool.h>
bool isPrime(long n) {
if ((n & 1) == 0)
return false;
for (long i=3; i*i <= n; i += 2)
if ((n % i) == 0)
return false;
return true;
}
int main (int argc, char **argv) {
int id, numThreads;
char results[200] = "[------------------------------------------------------------]";
char threads[200] = "[------------------------------------------------------------]";
long numbers[100];
printf("results = %s\n", results);
printf("threads = %s\n", threads);
for (int i = 0; i < 100; ++i)
numbers[i] = 100000000000001l + 2*i;
omp_set_num_threads(3);
int count = 0;
#pragma omp parallel for private(id) schedule(dynamic) reduction(+: count)
for (int i = 0; i < 60; ++i) {
id = omp_get_thread_num();
bool p = isPrime(numbers[i]);
results[1 + i] = (p ? '1' : '0');
threads[1 + i] = (char)(id + '0');
if (p)
++count;
}
printf("results = %s\n total number of primes found; %d\n", results, count);
printf("threads = %s\n", threads);
}
Vaja8
Razdeljevanje neodvisnih delov programa, med niti se da opraviti še na tretji način, in sicer z uporabo sekcij. V kodi je prikazana osnovna uporaba, ki ne zahteva dodatnih pojasnil. Dodati pa je treba le to, da je število sekcij neodvisno od števila niti, oziroma od števila jeder, ki so na voljo na posameznem sistemu. Če je niti več kot sekcij, potem bodo nekatere niti ostale brez dela. Če je sekcij več kot niti, potem bodo pa posamezne niti dobile v procesiranje več sekcij. Vrstni red v katerem se bodo sekcije izvedle ni definiran – navsezadnje se bodo izvajale vzporedno na več nitih hkrati.
Vaja9
V osnovi ni možno gnezditi omp parallel deklaracij. Kako torej izkoristiti neodvisnost dveh blokov programa in ene zanke? Na spodaj prikazan način. Uporaba nowait pove prevajalniku, da sme z prostimi nitmi še pred končanjem nekega vzporednega bloka programa (velja tako za najbolj osnoven parallel blok, kot tudi za for zanko in sections blok) nadaljevati naslednje vzporedne bloke. Če ne napišemo nowait bo namreč program čakal na točki, kjer se niti združijo nazaj v eno samo tako dolgo, dokler ne bodo vse niti končale z delom. Z nowait lahko enostavno in varno združujemo neodvisne bloke programa različnih tipov.
Sicer je možno tudi gnezdenje omp parallel pragem, a je treba to prej omogočiti s klicem funkcije omp_set_nested(true), a je ob tem potrebno obilo pazljivosti. Ob omogočenem gnezdenju namreč lahko spišemo rekurzivno funkcijo, ki v v sakem koraku naredi nekaj novih niti. Ob dovolj globokem izvajanju take funkcije lahko veliko število niti zabaše sistem do te mere, da se program obesi ali pa zelo destabilizira operacijski sistem.
#include stdio.h>
#include omp.h>
int main (int argc, char **argv) {
#pragma omp parallel num_threads(4)
{
#pragma omp sections nowait
{
#pragma omp section
{
printf("Thread #%d is here\n", omp_get_thread_num());
}
#pragma omp section
{
printf("While thread #%d is here\n", omp_get_thread_num());
}
}
#pragma omp for
for (int i=0; i < 10; ++i) {
printf("#%d is looping; ", omp_get_thread_num());
}
printf("\n");
}
}
Vaja10
V tej vaji lahko preizkušamo različne oblike gnezdenja omp parallel pragem.
#include stdio.h>
#include omp.h>
void function(int i, char* threads) {
#pragma omp parallel for
for (int j=0; j < 6; ++j) {
threads[(i*6)+j+1] = (char)('0'+omp_get_thread_num());
}
}
int main (int argc, char **argv) {
char results[200] = "[------------------------------------------------------------]";
char threads[200] = "[------------------------------------------------------------]";
omp_set_num_threads(4);
//#pragma omp parallel num_threads(2)
{
//#pragma omp for
for (int i=0; i < 10; ++i) {
function(i, threads);
/*
#pragma omp for
for (int j=0; j < 6; ++j) {
threads[(i*6)+j+1] = (char)('0'+omp_get_thread_num());
}
*/
}
}
printf("results = %s\n", results);
printf("threads = %s\n", threads);
}
Vaja11
V tej vaji je opisana še zadnja funkcija iz začetnega tečaja openmp. To je funkcija za merjenje časa – omp_get_wtime(). V tej vaji napišemo funkcijo delay, ki ponazarja časovno zahtevno opravilo. To funkcijo kličemo iz glavne zanke programa. Preizkušamo lahko koliko časa se izvaja program ob različnem številu uporabljenih niti (to je kar parameter, ki ga lahko prek ukazne vrstice podamo programu), različnih schedule načinih ter različno podanih parametrih delay funkciji. Hkrati lahko vidimo tudi katera nit dobi v procesiranje določen del zanke. Za to vajo je priporočeno veliko igranja s parametri in opazovanja rezultatov.
#include stdio.h>
#include stdlib.h>
#include omp.h>
void delay(int millis) {
double start = omp_get_wtime();
for (; ; ) {
double end = omp_get_wtime();
if ((end - start) > (millis*0.001))
break;
}
}
int main (int argc, char **argv) {
char threads[200] = "[------------------------------------------------------------]";
int maxNum, numThreads;
if (argc > 1)
numThreads = atoi(argv[1]);
else
numThreads = omp_get_num_threads();
if (argc > 2)
maxNum = atoi(argv[2]);
else
maxNum = 60;
omp_set_num_threads(numThreads);
double start = omp_get_wtime();
#pragma omp parallel
{
#pragma omp for schedule(dynamic)
for (int i=0; i < maxNum; ++i) {
delay((i*3)%maxNum);
threads[1+i] = (char)('0'+omp_get_thread_num());
}
}
double end = omp_get_wtime();
printf("threads = %s\n", threads);
printf("time taken = %.4f\n", (end - start));
printf("time resolution = %f\n", omp_get_wtick());
}
BranchAndBound
Nazadnje, na željo obiskovalcev še en preprost branch-and-bound (razveji in omeji) algoritem za iskanje največje klike v grafu, paraleliziran z uporabo OpenMP. Algrotirem ni optimiran in le prikazuje možen način varne paralelizacije takih tipov algoritmov.
V tem algoritmu lahko najdemo uporabo novega OpenMP konstrukta – task. Task naredi novo nit, v kateri požene kodo, ki sledi task pragmi. V bistvu je taka definicija malo poenostavljena a lahko služi kot prvi približek. Bolj natančno rečeno pa so taski le definicije dela programa, ki se lahko izvaja povsem asinhrono, in ki ga OpenMP izvede takrat ko ima na voljo prosto nit, ga lahko preklada med različnimi nitmi itd. Da bi sinhronizirali kodo lahko kličemo pragma omp taskwait, ki ustavi program, dokler se vsi taski ne končajo.
Še en konstrukt je nov – critical, ki predstavlja sinhronizacijski mehanizem za zaščito globalnih spremenljivk. Critical poskrbi, da se naslednji blok kode izvede brez prekinitev znotraj ene niti. V blok, ki ga zaznamuje critical sme vstopiti naenkrat le ena nit. Tako se tak blok kode zaščiti pred hkratnim branjem ali pisanjem več niti. Pri uporabi sinhronizacijskih mehanizmov, kot sta taskwait in critical je treba upoštevati, da lahko močno upočasnita izvajanje. Critical tako res poskrbi za varno uporabo globlanih spremenljivk vendar včasih za hudo ceno. Ko se je namesto uporabe critical možno uporabi globalnih spremenljivk ogniti, je v večini primerov to tudi priporočljivo storiti, čeprav lahko zakomplicira kodo.
Zadnji nov konstrukt je omp single, ki se lahko pojavi znotraj omp parallel bloka in povzroči da se sledeči ukaz ali celoten blok izvrši v le eni niti.
#include stdio.h>
#include stdlib.h>
#include time.h>
#include stdbool.h>
#include omp.h>
/*
* structure for keeping the algorithm state and relevant functions regarding the state
* */
#define MAX_NUM_NODES 1000
#define INVALID_NODE -1
struct State {
int cliqueSize, nodesLeft, graphSize, numBranches;
short clique[MAX_NUM_NODES];
short nodesToCheck[MAX_NUM_NODES];
};
void initState(struct State* state, int graphSize) {
if (state == 0)
return;
state->nodesLeft = graphSize;
state->graphSize = graphSize;
state->cliqueSize = 0;
state->numBranches = 0;
for (int i = 0; i < MAX_NUM_NODES; ++i) {
state->clique[i] = INVALID_NODE;
state->nodesToCheck[i] = (i < graphSize ? i : INVALID_NODE);
}
}
void copyState(struct State* from, struct State* to) {
to->cliqueSize = from->cliqueSize;
to->nodesLeft = from->nodesLeft;
to->graphSize = from->graphSize;
to->numBranches = 0;
for (int i = 0; igraphSize; ++i) {
to->clique[i] = from->clique[i];
to->nodesToCheck[i] = from->nodesToCheck[i];
}
}
/*
* Definition of a graph and functions dealing with graph (general and unrelated to clique)
* */
struct Graph {
short numNodes;
bool edges[MAX_NUM_NODES][MAX_NUM_NODES];
};
struct Graph* generateRandomGraph(int graphSize, float connectivityFactor) {
if ((graphSize > MAX_NUM_NODES) || (connectivityFactor >= 1))
return 0;
struct Graph* g = malloc(sizeof(struct Graph));
g->numNodes = graphSize;
int maxEdges = (graphSize * (graphSize-1)) / 2;
int wantEdges = (int)(maxEdges * connectivityFactor);
bool negateGraph = false;
for (int i = 0; i < graphSize; ++i) {
for (int j = 0; j < graphSize; ++j) {
g->edges[i][j] = false;
}
}
if (maxEdges - wantEdges < wantEdges) {
// negate graph to ease initializing edges
wantEdges = maxEdges - wantEdges;
negateGraph = true;
}
for (int i = 0; i < wantEdges;) {
short v1 = rand() % graphSize;
short v2 = (v1 + 1 + (rand() % (graphSize-1))) % graphSize;
if (g->edges[v1][v2] == false) {
++i;
g->edges[v1][v2] = true;
g->edges[v2][v1] = true;
}
}
if (negateGraph) {
for (int i = 0; i < graphSize; ++i) {
for (int j = 0; j < graphSize; ++j) {
g->edges[i][j] = (i == j ? false : !g->edges[i][j]);
}
}
}
return g;
}
/*
* Branch and bound maximum clique algorithm (very basic implementation)
* */
void keepOnlyNeighbours(short node, struct State* state, struct Graph* g) {
int maxNodeNum = state->nodesLeft-1;
for (int i = maxNodeNum; i >= 0; --i) {
if (!(g->edges[node][state->nodesToCheck[i]])) {
// i-th node left is not a neighbour of node
state->nodesToCheck[i] = state->nodesToCheck[maxNodeNum];
maxNodeNum--;
}
}
state->nodesLeft = maxNodeNum+1;
}
// return true if the branch can be eliminated (bound condition is sattisfied)
bool bound(struct Graph* g, struct State* state, int* maxCliqueSize) {
// note that this is a basic, not very smart bound
return ((state->nodesLeft + state->cliqueSize) <= *maxCliqueSize);
}
void branch(struct Graph* g, struct State* state, int* maxCliqueSize) {
state->numBranches++;
while (!(bound(g, state, maxCliqueSize))) {
// branch on this node:
state->nodesLeft--;
short node = state->nodesToCheck[state->nodesLeft];
// make copy of state to ease backtracking
struct State* stateCopy = malloc(sizeof(struct State));
copyState(state, stateCopy);
// go down the branch with the node added to clique
state->clique[state->cliqueSize] = node;
state->cliqueSize++;
if (*maxCliqueSize < state->cliqueSize) {
#pragma omp critical
{
if (*maxCliqueSize < state->cliqueSize) // another check (maxCliqueSize could be modified on multithreaded environment in the meantime)
*maxCliqueSize = state->cliqueSize;
}
}
keepOnlyNeighbours(node, state, g);
branch(g, state, maxCliqueSize);
if (stateCopy->nodesLeft > 0) {
branch(g, stateCopy, maxCliqueSize);
state->numBranches += stateCopy->numBranches;
}
free(stateCopy);
}
}
int maxClique(struct Graph* g, struct State* state) {
initState(state, g->numNodes);
int maxCliqueSize = 0;
branch(g, state, &maxCliqueSize);
return maxCliqueSize;
}
/*
* OpenMP parallel branch-and-bound
* */
int maxCliquePara(struct Graph* g, struct State* state) {
initState(state, g->numNodes);
// maximum clique size becomes a global variable
int maxCliqueSize = 0;
// change one level of recursion into a loop
#pragma omp parallel
{
#pragma omp single
{
printf(" running on %d threads\n performed this many branches: ", omp_get_num_threads());
struct State s;
for (int i = 0; state->nodesLeft>0; ++i) {
state->nodesLeft--;
short node = state->nodesToCheck[state->nodesLeft];
// make copy of state to ease backtracking
copyState(state, &s);
// go down the branch with the node added to clique
state->clique[state->cliqueSize] = node;
state->cliqueSize++;
keepOnlyNeighbours(node, state, g);
#pragma omp task firstprivate(s)
{
branch(g, &s, &maxCliqueSize);
printf("%d ", s.numBranches);
#pragma omp atomic
state->numBranches += s.numBranches;
}
}
}
if (maxCliqueSize < state->cliqueSize) {
#pragma omp critical
{
if (maxCliqueSize < state->cliqueSize) // another check (maxCliqueSize could be modified on multithreaded environment in the meantime)
maxCliqueSize = state->cliqueSize;
}
}
#pragma omp taskwait
#pragma omp single
printf("\n");
}
return maxCliqueSize;
}
/*
* various functions and main
* */
float seconds(time_t t1, time_t t2) {
return (t2-t1)/(float)CLOCKS_PER_SEC;
}
int main(int argc, char** argv) {
int graphSize;
if (argc > 1)
graphSize = atoi(argv[1]);
else
graphSize = 70;
int randSeed;
if (argc > 2)
randSeed = atoi(argv[2]);
else
randSeed = 10;
srand(randSeed);
time_t timeStartGraphInit = clock();
struct Graph* graph = generateRandomGraph(graphSize, 0.93f);
printf("Graph initialization took %f s\n", seconds(timeStartGraphInit, clock()));
{
time_t timeStartBandB = clock();
struct State state;
int maxSize = maxClique(graph, &state);
printf("Branch-and-bound took %f s and found clique of size %d in %d branches\n", seconds(timeStartBandB, clock()), maxSize, state.numBranches);
}
{
time_t timeStartBandB = clock();
double ompTimeStart = omp_get_wtime();
struct State state;
int maxSize = maxCliquePara(graph, &state);
printf("Parallel Branch-and-bound took %f s and found clique of size %d in %d branches\n", omp_get_wtime()-ompTimeStart, maxSize, state.numBranches);
printf("In total, threads used %f s of processor time\n", seconds(timeStartBandB, clock()));
}
}
Nazadnje še en link do zelu uporabnega ‘plonk listka’ za OpenMP, kjer lahko najdemo zgoščene podatke o vseh OpenMP funkcijah, direktivah, sistemskih spremenljivkah, itd:
http://openmp.org/mp-documents/OpenMP3.1-CCard.pdf
Sicer je več stvari dostopno iz osnovne strani OpenMP
| Priponka | Velikost |
|---|---|
| 3.74 KB | |
| 3.97 KB | |
| 2.17 KB | |
| 781.12 KB | |
| 488.11 KB |
