- Predstavitev
- Uporaba
- Dostop
- Programski jeziki in knjižnice
- modules
- Nadzornik računskih virov SLURM
- TotalView
- VisIt
- IOzone test
- OpenFOAM
- ppgplasma
- Inkscape
- LaTeX in SVG
- Access
- Analiza, razčlenitev in razhroščevanje
- Ansys
- BIT1
- Cluster Management Utility
- DDT
- Eclipse
- Elmer
- Goldfire Innovator
- MPI
- Mathematica
- NX shadow
- OpenMP
- Platform Managment Console
- Pošta
- R
- Subversion
- UGS NX
- Projekti in dogodki
- Prijava
- Wiki
Main menu
Nahajate se tukaj
Obremenjena elastična konzola
Uzračunali bomo upogib nosilca in napetost zaradi obtežbe, ob predpostavki homogenega elastičnega materila. Izbrali bomo nosilec iz borovega lesa kvadraste oblike, dolžine 1 metra, debeline 5 cm in širine 10 cm. Nosilec je na eni strani togo vpet v zid, na drugi pa obtežen z silo 2000 N. Borov les je gostote 550 kg/m3, Posionov količnik je 0.37, elastični modul pa 10E9 N/m2.
- Odpremo terminalsko okno in zaženemo:
$ single
Job XXXX is submited to default queue – interactive
Waiting for dispatch ...
Starting on cnXX
$ module load elmergui
Loading qwt/6.0.2
Loading vtk/5.10.1
Loading ftgl/2.1.3-rc5
Loading qt/4.8.4
Loading paraview/3.98
Loading opencascade/6.5.5
Loading elmer/7.0
Loading elmergui/7.0
$ ElmerGUI - V meniju programa ElmerGUI izberemo:
File -> Open
beam3d.grdDatoteka se nahaja se v 'elmerlab/lab03'.
V ElmerGUI oknu se prikaže geometrija objekta z generirano mrežo končnih elementov.
Povečamo ElmerGUI okno preko celega ekrana
Razotiramo objekt v približno pozicijo, kot prikazuje slika:
Premikanje objekta:
Z vrtenjem koleščka (naprej/nazaj) miške zumiramo objekt (prinližujemo/oddaljujemo)
- Z pritiskom leve miškine tipke in istočasnim premikom miške (gor/dol) rotiramo objekt okoli horizontalne osi.
- Z pritiskom leve miškine tipke in istočasnim premikom miške (levo/desno) rotiramo objekt okoli vertkalne osi.
- Postavimo objekt v približno pozicijo, kot prikazuje spodnja slika:
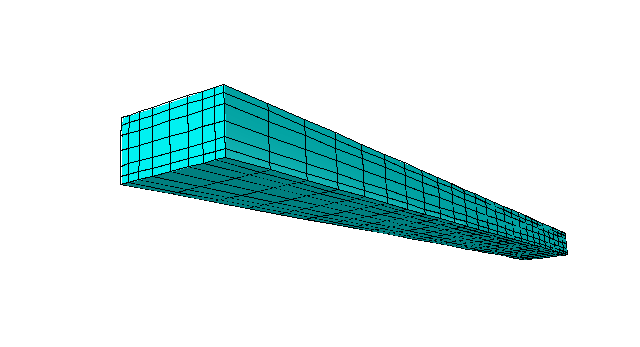 .
.
- Ko imamo mrežo začnemo z podajanjem podatkov preko modelnega menia v smeri od vrha proti dnu.
- Definiramo nastavitve povezane z celotno simulacijo. Naš problem je stacionarni v 3d kartezičnih koordinatah:
Model -> Setup
Simulation Type = Steady state
Steady state max. Iter =1
Coordinate mapping = 1 2 3
Apply - Definicija enačb:
Model -> Equation
Add
Name = Linear Elasticity (Korigiramo ime 'Equation 1' na 'Linear Elasticity')
Apply to bodies = Body 1 (tj postavimo kljukico)
Izberemo jeziček ‘Heat Equation’
Active = on (tj postavimo kljukico)
Calculate Stresses = on
Edit Solver Settings
Linear System
Method = Iterative / GCR
Preconditioning = ILU1
Nonlinear system
Max. iterations = 1
Apply
Add
OK (V redu) - Definiramo material:
Model -> Material
Add
Name = Pine
General
Density =550
Linear Elasticity
Young Modulus = 10.0e9
Poisson ratio = 0.37
Apply to bodies = Body 1 (postavimo kljukico)
Add
OK (V redu) - Definiramo obtežbo. V našem primeru je lo lastna teža nosilca zaradi gravitacije (predpostavimo, da gravitacija deluje v -y smeri). Pri določitvi sile zato uporabimo MATC izraz za izračun volumske sile (produkt gravitacije in specifične teže).:
Model -> Body force
Add
Name = Gravity
Linear Elasticity
Force 2 = $ -9.81 * 550
Apply to bodies = Body 1 (postavimo kljukico)
Add
OK (V redu) - Definiramo robne pogoje. Imao dva robna pogoja. S prvim definiramo togo vpetost nosilca v zid (pomiki so nič), z drugim pa porazdelimo obtežbo 2000 N na površini nasprotne stranske ploskve konzole (0.05 m x 0.1m =0.005m2). Na to stransko ploskev tako deluje obtežba 400 000 N/m2 v negativni smeri y osi.
Model -> Boundary condition
Add
Name = Wall
Linear elasticity
Displacement 1 = 0.0
Displacement 2 = 0.0
Displacement 3 = 0.0
Add
New
Name = Mass
Linear elasticity
Force 2 = -4.0e5
OK (V redu) - Ker ne poznamo indeksov robnih ploskev robnih pogojev ne dodelimo v ‘Boundary condition’ meniju, temveč uporabimo grafičen način:
Model -> Set boundary properties (izberemo oz odkljukamo opcijo)
1. Dvokiknemo na ploskev, kjer je nosilec vpet v zid in preko menija določimo 'Boundary condition': Wall. Potrdimo izbiro (v redu).
2. Dvokiknemo ploskev nasprotni ploskvi vpetja nosilca v zid in preko menija doočimo 'Boundary conditions': Mass. Potrdimo izbiro (v redu). - Generiramo vhodno datoteko za program ‘ElmerSolver’:
Nastalo datoteko si lahko ogledamo z izbiro iz menija:Sif -> Generate
Datoteko lahko nato uredimo, ali zapustimo z ukazom ‘File->Quit’.Sif -> Edit
- Shranimo projekt (Podatke projekta lahko shranimo v poljubni vazi vnosa):
File -> Save Project
Za shranjevanje projekta izberemo poljuben direktorij (npr. poddirektorij 'ProjectFiles'), kamor želimo shraniti narejeno.Opomba: Podatke projekta lahko prikličemo z: File -> LoadProject in izberemo dorektorij, kamor smo podatke shranili.
- Izračunamo primer:
Run -> Start solver
- Za ogled rezultatov poženemo postprocesor:
Run -> postprocesor - V podprocesoju si ogledamo rezultate pomikov izračunanega nosilca. Maksimalni pomik znaša 0.063592 m oz zaokroženo 6.4 cm. V postprocesorju je prikazan pomik s pomočjo barvne skale na nedeformirani geomertriji. Za dober pregled s pomočjo puščic v oknu programa ElmerPost zasukamo nosiec tako, da je dolžina nosilca vzporedna barvni skali pomikov.
- Pomik lahko s pomočjo ukaznega jezika MATC v postprocesorju prikažemo tudi na deformirani geometriji.prikažemo Izračunan pomik lahko prikažemo na geometriji. To storimo tako, da v ukazni vrstici (enovrstično sivo polje spodnjega robu okna) programa ElmerPost vpišemo ukaza:
Za osvežitev grafike kliknemo na desno ikono v gornji vrstici okna programa ElmerPost in dobimo rezultate, kot jih prikazuje spodnja slika.math n0=nodes
math nodes=n0+Displacement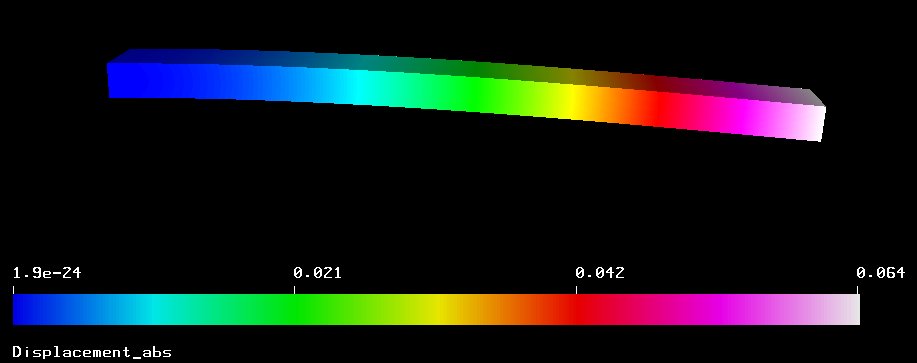
.
| Priponka | Velikost |
|---|---|
| 741 bytov |
